Solve the Problem $$f ( x ) = - \frac { 1 } { 8 } ( x - 1 ) ^ { 4 }$$

question 279

Multiple Choice

Solve the problem.
- $$f ( x ) = - \frac { 1 } { 8 } ( x - 1 ) ^ { 4 }$$
a. Identify the power function of the form $y = x ^ { n }$ that is the parent function to the given graph.
b. In order, outline the transformations that would be required on the graph of $y = x ^ { n }$ to make the graph of the given function.
c. Match the function with the graph.
i.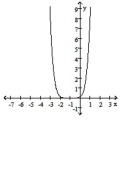


ii.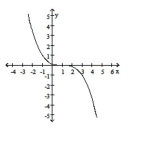


iii.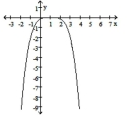


iv.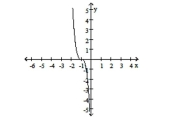

• A) a. \(y = x ^ { 4 }\) b. Shift \(y = x ^ { 4 }\) to the right 1 units. Shrink vertically by a factor of \(\frac { 1 } { 8 }\). Reflect across the \(x\)-axis. c. Graph iii.
• B) a. \(y = x ^ { 4 }\) b. Shift \(y = x ^ { 4 }\) to the left 1 units. Shrink vertically by a factor of \(\frac { 1 } { 4 }\). Reflect across the \(x\)-axis. c. Graph iii.
• C) a. \(y = x ^ { 4 }\) b. Shift \(y = x ^ { 4 }\) to the right 1 units. Shrink vertically by a factor of \(\frac { 1 } { 8 }\). Reflect across the \(x\)-axis. c. Graph ii.
• D) a. \(y = x ^ { 4 }\) b. Shift \(y = x ^ { 4 }\) to the left 1 units. Shrink vertically by a factor of \(\frac { 1 } { 4 }\). c. Graph i.

---

Definitions:

Probability Sampling

Type of sampling procedure in which one is able to specify the probability that any member of the populationwill be included in the sample.

Specific Population

A specific population refers to a defined group of individuals who share one or more characteristics for the purposes of research or study.

Precise Statements

Clearly defined and unambiguous declarations that convey specific information accurately.

Cluster Sampling

An approach to sampling in which the entire population is split into various segments, with a random selection of these segments being picked for examination.