SCENARIO 14-16
What Are the Factors That Determine the Acceleration $Y$

question 21

True/False

SCENARIO 14-16
What are the factors that determine the acceleration time (in sec.) from 0 to 60 miles per hour of a
car? Data on the following variables for 30 different vehicle models were collected: $Y$ (Accel Time): Acceleration time in sec.
$X _ { I }$ (Engine Size): c.c.
$X _ { 2 }$ (Sedan): 1 if the vehicle model is a sedan and 0 otherwise

The regression results using acceleration time as the dependent variable and the remaining variables as the independent variables are presented below.

$\begin{array}{lr}\hline{\text { Regression Statistics }} \\\hline \text { Multiple R } & 0.6096 \\\text { R Square } & 0.3716 \\\text { Adjusted R Square } & 0.3251 \\\text { Standard Error } & 1.4629 \\\text { Observations } & 30 \\\hline\end{array}$

ANOVA



$\begin{array}{lrrrrrr}\hline & \text { Coefficients } & \text { Standard Error } & \text { t Stat } & \text { P-value } & \text { Lower 95\% } & \text { Upper 95\% } \\\hline \text { Intercept } & 7.1052 & 0.6574 & 10.8086 & 0.0000 & 5.7564 & 8.4540 \\\text { Engine Size } & -0.0005 & 0.0001 & -3.6477 & 0.0011 & -0.0008 & -0.0002 \\\text { Sedan } & 0.7264 & 0.5564 & 1.3056 & 0.2027 & -0.4152 & 1.8681 \\\hline\end{array}$


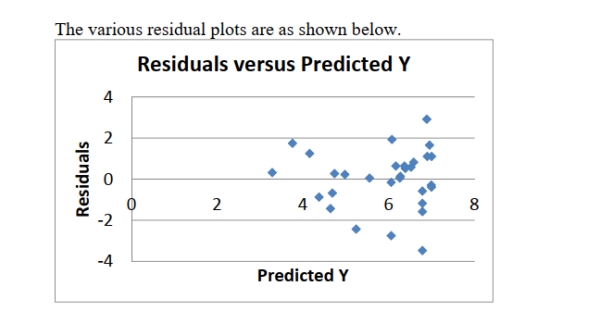
-Referring to Scenario 14-16, the error appears to be left-skewed.

---

Definitions:

Potential Profit

The projected or anticipated profit from a business activity or investment, considering current or expected conditions.

Transfer Price

Transfer price refers to the price at which goods and services are sold between departments or subsidiaries within the same company.

Selling Division

The division or section of a company responsible for sales activities and interfacing with customers to sell products or services.

Buying Division

A department or segment within a company responsible for purchasing goods, materials, or services.