A Hypothesis Testing Situation Is Given $$\begin{array} { l } \mathrm { H } _ { 0 } : \mu = 472 \\ \mathrm { H } _ { \mathrm { a } } : \mu \neq 472 . \end{array}$$

question 53

Essay

A hypothesis testing situation is given. The population standard deviation, sample size, and significance level are given.Complete the table to give the probability of a Type II error and the power for each of the given values of µ. Use the table to draw the power curve.
-In 1990, the average math SAT score for students at one school was 472. Five years later, a teacher wants to perform a hypothesis test to determine whether the average SAT score of students at the school has changed from the 1990 mean of 472. Preliminary data analyses indicate that it is reasonable to apply a z-test. The hypotheses are $$\begin{array} { l } \mathrm { H } _ { 0 } : \mu = 472 \\ \mathrm { H } _ { \mathrm { a } } : \mu \neq 472 . \end{array}$$ Assume that $\sigma = 74 , \mathrm { n } = 54$ , and the significance level is $0.01$ . Find the probability of a Type II error and the power for 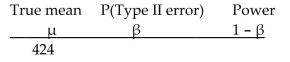$\mu = 424,430,440,450,460,470,474,484,494,504,514,520$ . 430 440 450 460 470 474 484 494 504 514 520

---

Definitions:

Lysine

An essential amino acid that the body cannot synthesize, important for protein synthesis and various metabolic processes.

Anorexia Nervosa

An eating disorder characterized by an extreme fear of gaining weight and a distorted body image, leading to severe weight loss.

Bulimia Nervosa

An eating disorder marked by periods of binge-eating followed by purging to avoid weight gain.

Eating Pattern

An individual’s habitual dietary intake, including the timing, amount, and types of food consumed.