Solve the System to Find W 1 and W 2\[\frac { \sqrt { 3 } } { 2 } \left( W _ { 1 } + W _ { 2 } \right) = 105\]

The Answer of Solve the System to Find W 1 and W 2\[\frac { \sqrt { 3 } } { 2 } \left( W _ { 1 } + W _ { 2 } \right) = 105\]

Solve the System to Find W 1 and W 2\[\frac { \sqrt { 3 } } { 2 } \left( W _ { 1 } + W _ { 2 } \right) = 105\]

The Answer of Solve the System to Find W 1 and W 2\[\frac { \sqrt { 3 } } { 2 } \left( W _ { 1 } + W _ { 2 } \right) = 105\]

Solved

Solve the System to Find W₁ and W₂ $\frac { \sqrt { 3 } } { 2 } \left( W _ { 1 } + W _ { 2 } \right) = 105$

question 361

Multiple Choice

Solve the system to find W₁ and W₂.
-Linear systems occur in the design of roof trusses for new homes and buildings. The simplest type of roof truss is a triangle. The truss shown in the figure is used to frame roofs of small buildings. If
A force of 105 pounds is applied at the peak of the truss, then the forces or weights W1 and W2
Exerted parallel to each rafter of the truss are determined by the following linear system of
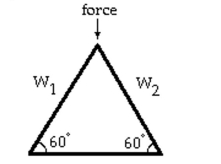
Equations. $Solve the system to find W<sub>1</sub> and W<sub>2</sub>. -Linear systems occur in the design of roof trusses for new homes and buildings. The simplest type of roof truss is a triangle. The truss shown in the figure is used to frame roofs of small buildings. If A force of 105 pounds is applied at the peak of the truss, then the forces or weights W1 and W2 Exerted parallel to each rafter of the truss are determined by the following linear system of Equations. \frac { \sqrt { 3 } } { 2 } \left( W _ { 1 } + W _ { 2 } \right) = 105 W _ { 1 } - W _ { 2 } = 0 A) W _ { 1 } = 35 \mathrm { lb } ; W _ { 2 } = 35 \mathrm { lb } B) W _ { 1 } = 60.62 \mathrm { lb } ; W _ { 2 } = 52.5 \mathrm { lb } C) \mathrm { W } _ { 1 } = 60.62 \mathrm { lb } ; \mathrm { W } _ { 2 } = 60.62 \mathrm { lb } D) \mathrm { W } _ { 1 } = - 60.62 \mathrm { lb } ; \mathrm { W } _ { 2 } = - 60.62 \mathrm { lb }$
$\frac { \sqrt { 3 } } { 2 } \left( W _ { 1 } + W _ { 2 } \right) = 105$
$W _ { 1 } - W _ { 2 } = 0$

Distinguish between gender roles, gender identity, and gender stereotypes.

Explain the impact of social and environmental factors on gender development.

Define and differentiate between various intersex conditions.

Understand the societal evolution and cultural variations in gender roles.

Definitions:

Jurisdictions

The official power to make legal decisions and judgments, often within a specific geographic area or over a certain type of case.

Marketable Title

A title to real property that is free from significant defects, encumbrances, or liens, and can be easily sold or mortgaged.

Warranty

A guarantee, typically from a manufacturer or seller, that a product will meet certain standards of quality and reliability or that specific repair or replacement actions will be taken if it does not.

Condemned

Property that has been officially taken by a government for public use, or deemed unsafe or unfit for use, often through the process of eminent domain or as a result of health and safety inspections.

Solve the System to Find W1 and W2 32(W1+W2)=105\frac { \sqrt { 3 } } { 2 } \left( W _ { 1 } + W _ { 2 } \right) = 10523​​(W1​+W2​)=105

Definitions:

Solve the System to Find W₁ and W₂ $\frac { \sqrt { 3 } } { 2 } \left( W _ { 1 } + W _ { 2 } \right) = 105$