Solve the Problem $a , b , c$ , and D So That

question 188

Multiple Choice

Solve the problem.
-Use regression to find constants $a , b , c$ , and d so that $\mathrm { f } ( \mathrm { x } ) = \mathrm { a } \sin ( \mathrm { bx } + \mathrm { c } ) + \mathrm { d }$ models the data given below. Round all answers to 9 decimal places.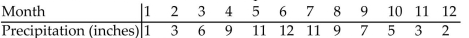

• A) \(4.708150061 ; 1.025102863 ; - 2.474285177 ; 7.076487153\)
• B) \(5.099259265 ; 0.531578044 ; - 1.738394218 ; 8.659926499\)
• C) \(5.277184939 ; 0.062976370 ; - 2.042562480 ; 6.904195597\)
• D) \(5.099259265 ; 0.531578044 ; - 1.738394218 ; 6.659926499\)

---

Definitions:

Degrees Of Freedom

The number of values in a calculation that are free to vary without violating any constraints, used to determine the shape of various statistical distributions.

Sample Mean

The mean of a dataset, found by adding up all the values and then dividing the total by the count of values in the set.

Standard Deviation

A measure of the amount of variation or dispersion in a set of values, showing how much the values differ from the mean.

Margin Of Error

An expression of the maximum expected difference between the true population parameter and a sample estimate of that parameter.