Solve
-If the Three Lengths of the Sides of a Triangle

question 283

Multiple Choice

Solve.
-If the three lengths of the sides of a triangle are known, Heron's formula can be used to find its area. and $c$ are the three lengths of the sides, Heron's formula for area is:
$$A = \sqrt { s ( s - a ) ( s - b ) ( s - c ) }$$
where $s$ is half the perimeter of the triangle, or $s = \frac { 1 } { 2 } ( a + b + c )$ .
Use this formula to find the area of the triangle if $a 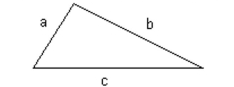= 9 \mathrm {~cm} , \mathrm {~b} = 11 \mathrm {~cm}$ and $c = 16 \mathrm {~cm}$ .

• A) \(3 \sqrt { 14 } \mathrm { sq } \mathrm { cm }\)
• B) \(18 \sqrt { 7 } \mathrm { sq } \mathrm { cm }\)
• C) \(18 \sqrt { 14 } \mathrm { sq } \mathrm { cm }\)
• D) \(180 \sqrt { 15 } \mathrm { sq } \mathrm { cm }\) , b,

---

Definitions:

Virtual Private Network

A technology that creates a safe, encrypted connection over a less secure network, such as the internet, to provide privacy and data security.

Access Codes

Passwords or numerical codes used to gain entry into secured systems or locations.

Local Network

refers to a network that connects computers and devices in a limited geographical area such as a home, school, computer laboratory, or office building, facilitating communication and resource sharing among devices within this area.

Computer Network

A set of computers connected together for the purpose of sharing resources, such as data, printers, and Internet connections.