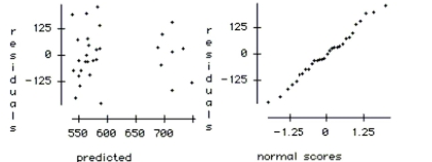
The Regression Below Predicts the Daily Number of Skiers Who $F$

question 6

Essay

The regression below predicts the daily number of skiers who visit a small ski resort based on three explanatory variables.
The data is a random sample of 30 days from the past two ski seasons. The variables are: SKIERS the number of skiers who visit the resort on that day
SNOW the number of inches of snow on the ground
TEMP the high temperature for the day in degrees $F$ .
WEEKDAY an indicator variable, weekday $= 1$ , weekend $= 0$
Dependent variable is Skiers
$R$ squared $= 25.4 \% \quad$ R squared (adjusted) $= 16.8 \%$
$s = 125.1$ with $30 - 4 = 26$ degrees of freedom



$\begin{array}{lrrrr}\text { Variable } & \text { Coefficient } & \text { SE(Coeff) } & \text { t-ratio } & \text { p-value } \\\text { Constant } & 559.869 & 76.78 & 7.29 & <0.0001 \\\text { Snow } & 1.424 & 2.70 & 0.53 & 0.6019 \\\text { Temp } & -1.604 & 2.77 & -0.58 & 0.5677 \\\text { Weekend } & 147.349 & 51.86 & 2.84 & 0.0086\end{array}$





-Compute a 95% confidence interval for the slope of the variable Weekend, and explain the
meaning of the interval in the context of the problem.

---

Definitions:

Pollution Abatement

The reduction or elimination of pollutants released into the environment, often through regulatory policies or technology changes.

Pigouvian Tax

A tax imposed on activities that generate negative externalities, aiming to correct an inefficient market outcome by increasing the cost to include the external costs.

CFCs

Chlorofluorocarbons; chemical compounds used in aerosol sprays and refrigerants that have been found to deplete the ozone layer.

Adverse Selection

A situation in which one party in a transaction has more information than the other, often leading to the selection of poorer-quality goods or higher-risk individuals.