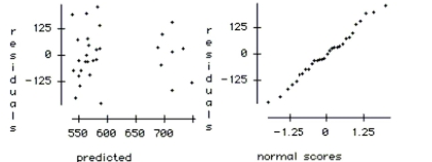
The Regression Below Predicts the Daily Number of Skiers Who $F$

question 6

Essay

The regression below predicts the daily number of skiers who visit a small ski resort based on three explanatory variables.
The data is a random sample of 30 days from the past two ski seasons. The variables are: SKIERS the number of skiers who visit the resort on that day
SNOW the number of inches of snow on the ground
TEMP the high temperature for the day in degrees $F$ .
WEEKDAY an indicator variable, weekday $= 1$ , weekend $= 0$
Dependent variable is Skiers
$R$ squared $= 25.4 \% \quad$ R squared (adjusted) $= 16.8 \%$
$s = 125.1$ with $30 - 4 = 26$ degrees of freedom



$\begin{array}{lrrrr}\text { Variable } & \text { Coefficient } & \text { SE(Coeff) } & \text { t-ratio } & \text { p-value } \\\text { Constant } & 559.869 & 76.78 & 7.29 & <0.0001 \\\text { Snow } & 1.424 & 2.70 & 0.53 & 0.6019 \\\text { Temp } & -1.604 & 2.77 & -0.58 & 0.5677 \\\text { Weekend } & 147.349 & 51.86 & 2.84 & 0.0086\end{array}$





-Compute a 95% confidence interval for the slope of the variable Weekend, and explain the
meaning of the interval in the context of the problem.

---

Definitions:

Insulin Levels

The level of insulin, a hormone made by the pancreas to control blood sugar levels, present in the blood.

Leptin

An agent released by fat tissues tasked with maintaining energy stability by reducing the sensation of appetite.

Body Fat

The portion of the human or animal body composed of fat tissues, serving as energy storage and insulation.

Puberty

The phase of life in which a child develops into an adult, marked by physical, emotional, and hormonal changes that prepare the body for reproduction.