The Regression Below Predicts the Daily Number of Skiers Who $F$

question 9

Essay

The regression below predicts the daily number of skiers who visit a small ski resort based on three explanatory variables.
The data is a random sample of 30 days from the past two ski seasons. The variables are: SKIERS the number of skiers who visit the resort on that day
SNOW the number of inches of snow on the ground
TEMP the high temperature for the day in degrees $F$ .
WEEKDAY an indicator variable, weekday $= 1$ , weekend $= 0$
Dependent variable is Skiers
$\mathrm { R }$ squared $= 25.4 \% \quad \mathrm { R }$ squared (adjusted) $= 16.8 \%$
$\mathrm { s } = 125.1$ with $30 - 4 = 26$ degrees of freedom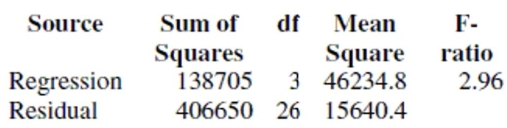



$\begin{array}{lrrrr}\text { Variable } & \text { Coefficient } & \text { SE(Coeff) } & \text { t-ratio } & \text { p-value } \\\text { Constant } & 559.869 & 76.78 & 7.29 & <0.0001 \\\text { Snow } & 1.424 & 2.70 & 0.53 & 0.6019 \\\text { Temp } & -1.604 & 2.77 & -0.58 & 0.5677 \\\text { Weekend } & 147.349 & 51.86 & 2.84 & 0.0086\end{array}$



-What is the predicted number of skiers for a Saturday with a temperature of 40° F. and a
snow cover of 25 inches?

---

Definitions:

Complex Environments

Complex environments refer to settings or systems with multiple interlinked components and variables, which are difficult to understand, predict, or control.

Finance

The study of money; how it’s made, how it’s lost, and how it’s managed.