Students a Growing School District Tracks the Student Population Growth $= 119.53 + 172.03$

question 97

Essay

Students A growing school district tracks the student population growth over the years
from 2008 to 2013. Here are the regression results and a residual plot. students $= 119.53 + 172.03$ year
Sample size: 6
$\mathrm { R } - \mathrm { sq } = 0.987$
students $= 119.53 + 172.03$ y
Sample size: 6
R-sq 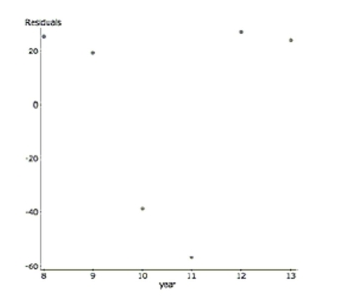$= 0.987$



a. Explain why despite a high R-sq, this regression is not a successful model.
To linearize the data, the log (base 10) was taken of the student population. Here are the results.
Dependent Variable: log(students) Sample size: 6
$$\mathrm { R } - \mathrm { sq } = 0.994$$
$\begin{array} { l r r } \text { Parameter } & \text { Estimate } & \text { Std. Err. } \\ \text { constant } & 2.871 & 0.0162 \\ \text { year } & 0.0389 & 0.00152 \end{array}$



b. Describe the success of the linearization.
c. Interpret R-sq in the context of this problem.
d. Predict the student population in 2014.

---

Definitions:

Statistics Canada

The national statistical office of Canada, responsible for producing statistics to help better understand the country, its population, resources, economy, society, and culture.

Mortality Data

Information and statistics on the incidence of death within a specified population.

Importance Gap

The discrepancy between the expected importance of an attribute or factor and its perceived performance, usually in the context of service or product evaluation.

Modern Technology

Contemporary tools, devices, and techniques used to facilitate tasks and solve problems in various domains, including communication, transportation, and healthcare.