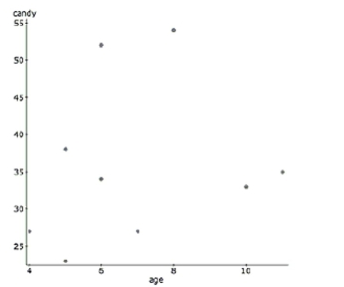
Halloween Is a Fun Night $R$ (Correlation Coefficient) $= \mathbf { 0 . 1 9 5 3 4 4 2 5 }$

question 24

Essay

Halloween is a fun night. It seems that older children might get more candy because they can travel further while
trick-or-treating. But perhaps the youngest kids get extra candy because they are so cute. Here are some data that examine
this question, along with the regression output. Dependent Variable: candy
Sample size: 9
$R$ (correlation coefficient) $= \mathbf { 0 . 1 9 5 3 4 4 2 5 }$
$\mathrm { R } - \mathrm { sq } = 0.038159375$
$s = 11.297554$
$\begin{array} { l r r } \text { Parameter } & \text { Estimate } & \text { Std. Err. } \\ \text { Intercept } & 13.569231 & 9.0783516 \\ \text { Age } & 3.4038462 & 1.0175376 \end{array}$


-The next day, a young girl reveals that her older brother also went trick-or-treating, but
didn't want to admit that he participated. He was added to the data set and these are the
results. Dependent Variable: candy
Sample size: 10
$R$ (correlation coefficient $) = 0.76362369$
$\mathrm { R } - \mathrm { sq } = 0.58312115$
$\mathrm { s } = 12.709041$
$\begin{array} { l r r } \text { Parameter } & \text { Estimate } & \text { Std. Err. } \\ \text { Intercept } & 13.569231 & 9.0783516 \\ \text { Age } & 3.4038462 & 1.0175376 \end{array}$


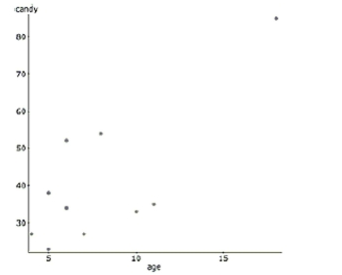
Describe the effect of this new candy collector on the regression model.

---

Definitions:

Capital Lease

A lease agreement in which the lessee essentially has the economic benefits and risks of ownership, often leading to the asset being recorded on the lessee's balance sheet.

Temporary Use

The use of an asset or resource for a limited period of time, not intended for long-term or permanent use.

Premium Amortization

Premium amortization is the process of gradually reducing the premium paid above the face value of a bond over its lifetime until it reaches its par value.

Bond Amortization Schedule

A table detailing each periodic payment on a bond issue through amortization, showing the amount of interest and principal included in each payment until the bond matures.