Penicillin Doctors Studying How the Human Body Assimilates Medication Inject $= 90.8 \% \quad$

question 537

Essay

Penicillin Doctors studying how the human body assimilates medication inject some
patients with penicillin, and then monitor the concentration of the drug (in units/cc) in the
patients' blood for seven hours. The data are shown in the scatterplot. First they tried to fit
a linear model. The regression analysis and residuals plot are shown. Dependent variable is:
Concentration
No Selector
R squared $= 90.8 \% \quad$ R squared (adjusted) $= 90.6 \%$
$s = 3.472$ with $43 - 2 = 41$ degrees of freedom

$\begin{array}{llrrr}\text { Source } & \text { Sum of Squares } & \text { df } & \text { Mean Square } & \text { F-ratio } \\\text { Regression } & 4900.55 & 1 & 4900.55 & 407 \\\text { Residual } & 494.199 & 41 & 12.0536 &\end{array}$


$\begin{array}{lllrc}\text { Variable } & \text { Coefficient } & \text { s.e. of Coeff } & \text { t-ratio } & \text { prob } \\\text { Constant } & 40.3266 & 1.295 & 31.1 & \leq 0.0001 \\\text { Time } & -5.95956 & 0.2956 & -20.2 & \leq 0.0001\end{array}$



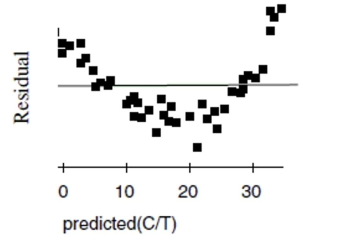
a. Find the correlation between time and concentration.
b. Using this model, estimate what the concentration of penicillin will be after 4 hours.
c. Is that estimate likely to be accurate, too low, or too high? Explain.
Now the researchers try a new model, using the re-expression log(Concentration). Examine
the regression analysis and the residuals plot below. Dependent variable is: $\quad$ LogCnn No Selector R squared $= 98.0 \% \quad$ R squared (adjusted) $= 98.0 \%$
$s = 0.0451$ with $43 - 2 = 41$ degrees of freedom

$\begin{array}{llrrr}\text { Source } & \text { Sum of Squares } & \text { df } & \text { Mean Square } & \text { F-ratio } \\\text { Regression } & 4.11395 & 1 & 4.11395 & 2022 \\\text { Residual } & 0.083412 & 41 & 0.002034 &\end{array}$

$\begin{array}{llllc}\text { Variable } & \text { Coefficient } & \text { s.e. of Coeff } & \text { t-ratio } & \text { prob } \\\text { Constant } & 1.80184 & 0.0168 & 107 & \leq 0.0001 \\\text { Time } & -0.172672 & 0.0038 & -45.0 & \leq 0.0001\end{array}$





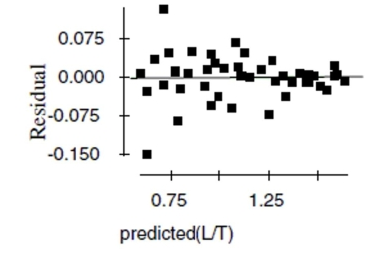
d. Explain why you think this model is better than the original linear model.
e. Using this new model, estimate the concentration of penicillin after 4 hours.

Recognize the role of critical thinking in nursing practice and support its development.

Apply principles of clinical judgment in responding to patient preferences in care plans, especially regarding lifestyle and diet.

Generalize clinical judgment models to enhance nursing practice.

Encourage critical thinking and learning from medication errors.

---

Definitions:

Peer Rejection

A situation in which a child or adolescent is systematically excluded or ostracized by their peers.

Problematic Adjustment

Problematic adjustment refers to difficulties or challenges in adapting to new or changing circumstances, environments, or roles, often resulting in stress or dysfunction.

Independence

The state or quality of being self-reliant and autonomous, often associated with making decisions without external influence.

Working Mother

A mother who engages in employment outside the home in addition to her family responsibilities.