Students a Growing School District Tracks the Student Population Growth $= 119.53 + 172.03$

question 602

Essay

Students A growing school district tracks the student population growth over the years
from 2008 to 2013. Here are the regression results and a residual plot. students $= 119.53 + 172.03$ year
Sample size: 6
$\mathrm { R } - \mathrm { sq } = 0.987$


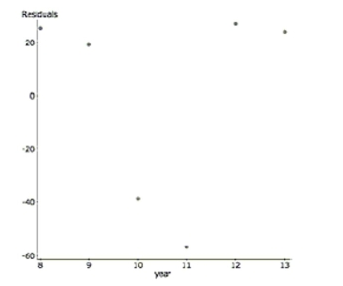
a. Explain why despite a high $\mathrm { R } - \mathrm { sq }$ , this regression is not a successful model.
To linearize the data, the $\log$ (base 10 ) was taken of the student population. Here are the results.
Dependent Variable: $\log$ (students)
Sample size: 6
$$\mathrm { R } - \mathrm { sq } = 0.994$$
$\begin{array} { l r r } \text { Parameter } & \text { Estimate } & \text { Std. Err. } \\ \text { constant } & 2.871 & 0.0162 \\ \text { year } & 0.0389 & 0.00152 \end{array}$

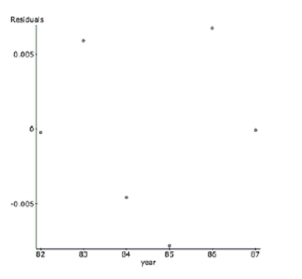
b. Describe the success of the linearization.
c. Interpret R-sq in the context of this problem.
d. Predict the student population in 2014.

---

Definitions:

Straight Voting

A voting system for electing directors where shareholders must vote for each board position individually, allowing majority shareholders to dominate elections.

Cumulative Voting

Cumulative Voting is a voting system that allows shareholders to allocate their votes in a flexible manner among one or more candidates during the election of a company's directors, enhancing minority shareholders' representation.

Growing Perpetuity

A constant stream of cash flows without end that is expected to rise indefinitely.