Students a Growing School District Tracks the Student Population Growth $= 119.53 + 172.03$

question 602

Essay

Students A growing school district tracks the student population growth over the years
from 2008 to 2013. Here are the regression results and a residual plot. students $= 119.53 + 172.03$ year
Sample size: 6
$\mathrm { R } - \mathrm { sq } = 0.987$


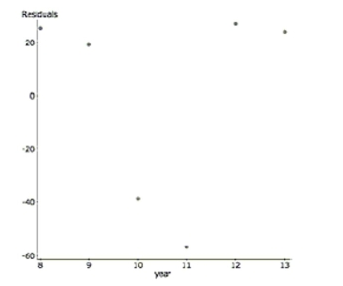
a. Explain why despite a high $\mathrm { R } - \mathrm { sq }$ , this regression is not a successful model.
To linearize the data, the $\log$ (base 10 ) was taken of the student population. Here are the results.
Dependent Variable: $\log$ (students)
Sample size: 6
$$\mathrm { R } - \mathrm { sq } = 0.994$$
$\begin{array} { l r r } \text { Parameter } & \text { Estimate } & \text { Std. Err. } \\ \text { constant } & 2.871 & 0.0162 \\ \text { year } & 0.0389 & 0.00152 \end{array}$

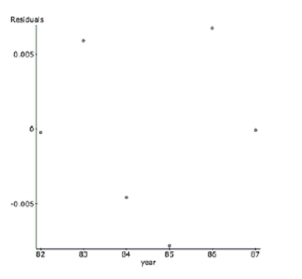
b. Describe the success of the linearization.
c. Interpret R-sq in the context of this problem.
d. Predict the student population in 2014.

---

Definitions:

Theory

A systematically organized set of concepts, explanations, and propositions that explain or predict events or situations by specifying relations among variables.

Visual System

The part of the central nervous system that allows organisms to see, including the eyes, optic nerves, and visual areas of the brain.

Fully Develop

Fully Develop means to reach the maximum potential or maturity in physical, mental, emotional, or cognitive aspects.

Months

Units of time, typically consisting of 28 to 31 days, used in calendars to divide the year into twelve periods.