The Regression Below Predicts the Daily Number of Skiers Who $F$

question 6

Essay

The regression below predicts the daily number of skiers who visit a small ski resort based on three explanatory variables.
The data is a random sample of 30 days from the past two ski seasons. The variables are: SKIERS the number of skiers who visit the resort on that day
SNOW the number of inches of snow on the ground
TEMP the high temperature for the day in degrees $F$ .
WEEKDAY an indicator variable, weekday $= 1$ , weekend $= 0$
Dependent variable is Skiers
$R$ squared $= 25.4 \% \quad$ R squared (adjusted) $= 16.8 \%$
$s = 125.1$ with $30 - 4 = 26$ degrees of freedom



$\begin{array}{lrrrr}\text { Variable } & \text { Coefficient } & \text { SE(Coeff) } & \text { t-ratio } & \text { p-value } \\\text { Constant } & 559.869 & 76.78 & 7.29 & <0.0001 \\\text { Snow } & 1.424 & 2.70 & 0.53 & 0.6019 \\\text { Temp } & -1.604 & 2.77 & -0.58 & 0.5677 \\\text { Weekend } & 147.349 & 51.86 & 2.84 & 0.0086\end{array}$





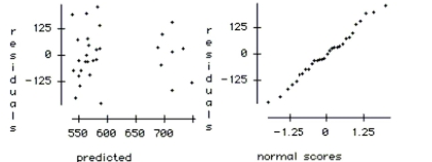
-Compute a 95% confidence interval for the slope of the variable Weekend, and explain the
meaning of the interval in the context of the problem.

Understand the role of managerial awareness in addressing individual differences within the workplace.

Grasp the significance of gender and cultural roles in shaping individual behavior in professional settings.

Recognize the contribution of personality traits and theories in understanding workplace dynamics and employee management.

Understand the influence of global cultural dimensions, including uncertainty avoidance, power distance, and cultural orientation, on personality and behavior within organizations.

---

Definitions:

Genitalia

The external and internal organs of the reproductive system in animals and humans.

Sexuality

The capacity for sexual feelings, including a person's sexual orientation, preferences, and practices.

Sexual Desires

The natural or instinctual attraction and longing for sexual activity or engagement, which varies widely among individuals.

Intersex

People do not fit conventional male or female sex categories. Often, intersex people do not have a sex chromosome that is XX or XY. Their genitals, reproductive system, and secondary sexual characteristics are not distinctly male or female in the conventional sense of the terms.