For Each Integer $n \geq 3$ , Let $P ( n )$

question 16

Essay

For each integer $n \geq 3$ , let $P ( n )$ be the equation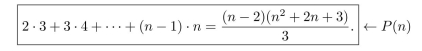

(Recall that by definition $\left. 2 \cdot 3 + 3 \cdot 4 + \cdots + ( n - 1 ) \cdot n = \sum _ { i = 3 } ^ { n } ( i - 1 ) \cdot i . \right)$
(a) Is $P ( 3 )$ true? Justify your answer.
(b) In the inductive step of a proof that $P ( n )$ is true for all integers $n \geq 3$ , we suppose $P ( k )$ is true (this is the inductive hypothesis), and then we show that $P ( k + 1 )$ is true. Fill in the blanks below to write what we suppose and what we must show for this particular equation.
Proof that for all integers $k \geq 3$ , if $P ( k )$ is true then $P ( k + 1 )$ is true:
Let $k$ be any integer that is greater than or equal to 3 , and suppose that____ We must show that_____
(c) Finish the proof started in (b) above.

---

Definitions:

Unit Contribution Margin

The difference between the selling price per unit and the variable cost per unit. This figure shows how much each unit contributes to covering fixed costs and generating profit.

Fixed Costs

Expenses that do not change in total as production volume increases or decreases, such as rent and salaries.

Safety Margin

The difference between the actual level of sales or production and the break-even point, measuring the cushion a company has before it incurs losses.

Break Even Point

The financial analysis term where total revenues equal total expenses, and there is no profit or loss.