Solve Problems Involving Systems Without Unique Solutions
Solve the Problem $t + 8$

question 128

Multiple Choice

Solve Problems Involving Systems Without Unique Solutions
Solve the problem using matrices.
-The figure below shows the intersection of three one-way streets. To keep traffic moving, the number of cars per minute entering an intersection must equal the number of cars leaving that intersection. Set up a
System of equations that keeps traffic moving, and use Gaussian elimination to solve the system. If
Construction limits z to t cars per minute, how many cars per minute must pass through the other
Intersections to keep traffic moving?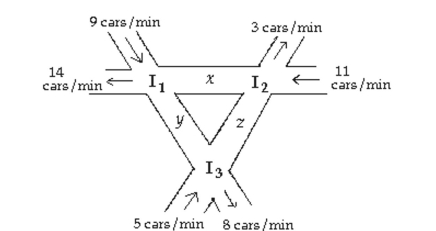

• A) \(t + 8\) cars \(/ \mathrm { min }\) between \(\mathrm { I } _ { 2 }\) and \(\mathrm { I } _ { 1 } ; \mathrm { t } + 3 \mathrm { cars } / \mathrm { min }\) between \(\mathrm { I } _ { 1 }\) and \(\mathrm { I } _ { 3 }\)
• B) \(t + 1\) cars \(/ \mathrm { min }\) between \(\mathrm { I } _ { 2 }\) and \(\mathrm { I } _ { 1 } ; \mathrm { t } + 4 \mathrm { cars } / \mathrm { min }\) between \(\mathrm { I } _ { 1 }\) and \(\mathrm { I } _ { 3 }\)
• C) \(t - 2\) cars \(/ \mathrm { min }\) between \(\mathrm { I } _ { 2 }\) and \(\mathrm { I } _ { 1 } ; \mathrm { t } + 1\) cars/min between \(\mathrm { I } _ { 1 }\) and \(\mathrm { I } _ { 3 }\)
• D) \(t + 2\) cars \(/ \mathrm { min }\) between \(\mathrm { I } _ { 2 }\) and \(\mathrm { I } _ { 1 } ; \mathrm { t } - 3 \mathrm { cars } / \mathrm { min }\) between \(\mathrm { I } _ { 1 }\) and \(\mathrm { I } _ { 3 }\)

---

Definitions:

Consistent Principle

A concept or rule that remains uniform and unchanged across different contexts or situations, ensuring coherence and reliability in application.

Essential Attributes

Essential attributes refer to the fundamental or inherent qualities that define the nature of something.

Consistent Principle

A rule or standard that remains uniform and unchanged over time, ensuring reliability and predictability in reasoning or behavior.

Jointly Exhaustive

A characteristic of a set of categories or propositions that together cover all possible scenarios or outcomes, leaving no options unaccounted for.