The Following MINITAB Output Presents a Multiple Regression Equation $\hat { y } = b _ { 0 } + b _ { 1 } x _ { 1 } + b _ { 2 } x _ { 2 } + b _ { 3 } x _ { 3 }$

question 31

Multiple Choice

The following MINITAB output presents a multiple regression equation $\hat { y } = b _ { 0 } + b _ { 1 } x _ { 1 } + b _ { 2 } x _ { 2 } + b _ { 3 } x _ { 3 }$ $+ b _ { 4 } x _ { 4 }$ .
The regression equation is
$$\mathrm { Y } = 1.9568 + 1.7369 \mathrm { X } 1 + 1.1099 \mathrm { X } 2 - 1.2672 \mathrm { X } 3 + 1.6080 \mathrm { X } 4$$
$\begin{array}{lllll}\text { Predictor } & \text { Coef } & \text { SE Coef } & \text { T } & \text { P } \\\text { Constant } & 1.9568 & 0.8248 & 1.1277 & 0.345 \\\text { X1 } & 1.7369 & 0.7980 & 3.4296 & 0.004 \\\text { X2 } & 1.1099 & 0.7500 & -3.2529 & 0.006 \\\text { X3 } & -1.2672 & 0.7534 & 1.8730 & 0.076 \\\text { X4 } & 1.6080 & 0.8733 & -0.9328 & 0.349\end{array}$


$\text { Analysis of Variance }$
$\begin{array}{lccccc}\text { Source } & \text { DF } & \text { SS } & \text { MS } & \text { F } & \text { P } \\\text { Regression } & 4 & 503.9 & 126.0 & 5.0806 & 0.003 \\\text { Residual Error } & 40 & 990.4 & 24.8 & & \\\text { Total } & 44 & 1,494.3 & & & \\\hline\end{array}$

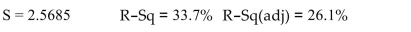
Predict the value of $\mathrm { y }$ when $x _ { 1 } = 1 , x _ { 2 } = 2 , x _ { 3 } = 3 , x _ { 4 } = 6$

• A) 9.798
• B) 9.8031
• C) 10.6228
• D) 11.7599

---

Definitions:

Perceptual Sets

Psychological mechanisms that influence how people perceive and interpret sensory information based on their expectations and prior experiences.

Internal Factor

An influence, element, or condition within an organization that affects its operations and outcomes.

Person Perception

The process of forming impressions and making judgments about other people's traits, intentions, and behaviors.

Perceiver Characteristics

Attributes or traits of the individual observing and interpreting others' behaviors, such as biases, attitudes, experiences, and personality, that affect their perceptions.