The Following MINITAB Output Presents a Multiple Regression Equatior $\hat { y }$

question 19

Multiple Choice

The following MINITAB output presents a multiple regression equatior $\hat { y }$ =b₀+b₁x₁+b₂x₂+b₃x₃+b₄x₄
The regression equation is
$$\mathrm { Y } = 5.5079 + 1.6552 \mathrm { X } 1 - 1.1088 \mathrm { X } 2 + 1.3981 \mathrm { X } 3 - 1.2465 \mathrm { X } 4$$

$\begin{array}{lllll}\text { Predictor } & \text { Coef } & \text { SE Coef } & \text { T } & \text { P } \\\text { Constant } & 5.5079 & 0.7640 & 1.1002 & 0.314 \\\text { X1 } & 1.6552 & 0.7032 & 3.1929 & 0.002 \\\text { X2 } & -1.1088 & 0.6023 & -3.2310 & 0.005 \\\text { X3 } & 1.3981 & 0.8970 & 1.8137 & 0.087 \\\text { X4 } & -1.2465 & 0.8251 & -1.1433 & 0.354\end{array}$



$\text { Analysis of Variance }$
$\begin{array}{lccccc}\text { Source } & \text { DF } & \text { SS } & \text { MS } & \text { F } & \text { P } \\\text { Regression } & 4 & 637.5 & 159.4 & 7.1480 & 0.003 \\\text { Residual Error } & 40 & 893.2 & 22.3 & & \\\text { Total } & 44 & 1,530.7 & & &\end{array}$

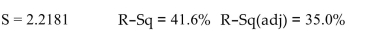
Let $\beta _ { 1 }$ be the coefficient $X _ { 1 }$ Test the hypothesis $H _ { 0 } : \beta _ { 1 } = 0$ rersus $H _ { 1 } : \beta _ { 1 } \neq 0 \text { at the } \alpha = 0.05$
level. What do you conclude?

• A) Do not H₀
• B) Reject H₀

---

Definitions:

Lateral Moraine

A ridge of debris deposited along the sides of a glacier, marking the previous extent of the glacier's reach.

Terminal Moraine

A moraine deposited at the point of furthest advance of a glacier or ice sheet, marking its maximum extent.

Kettle

A pitlike depression in glacial deposits, commonly a lake or swamp; formed by the melting of a large block of ice that had been at least partly buried in the glacial deposits.

Coastal Dunes

Sand formations located near coastlines, formed by the wind's movement of sand.