The Following MINITAB Output Presents a Multiple Regression Equatior $\hat { y }$

question 38

Multiple Choice

The following MINITAB output presents a multiple regression equatior $\hat { y }$ =b₀+b₁x₁+b₂x₂+b₃x₃+b₄x₄

The regression equation is
$$\mathrm { Y } = 2.5919 - 1.3391 \mathrm { X } 1 + 0.6212 \mathrm { X } 2 + 1.6435 \mathrm { X } 3 + 1.4269 \mathrm { X } 4$$

$\begin{array}{lllll}\text { Predictor } & \text { Coef } & \text { SE Coef } & \text { T } & \text { P } \\\text { Constant } & 2.5919 & 0.6269 & 1.1668 & 0.337 \\\text { X1 } & -1.3391 & 0.6716 & 3.5190 & 0.002 \\\text { X2 } & 0.6212 & 0.8488 & -3.2848 & 0.004 \\\text { X3 } & 1.6435 & 0.7934 & 1.8821 & 0.090 \\\text { X4 } & 1.4269 & 0.7679 & -0.9879 & 0.345\end{array}$




$\text { Analysis of Variance }$
$\begin{array}{lccccc}\text { Source } & \text { DF } & \text { SS } & \text { MS } & \text { F } & \text { P } \\\text { Regression } & 4 & 735.9 & 184.0 & 7.7311 & 0.003 \\\text { Residual Error } & 25 & 594.6 & 23.8 & & \\\text { Total } & 29 & 1,330.5 & & & \\\hline\end{array}$
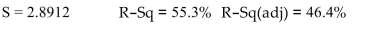
Let $\beta _ { 3 }$ be the coefficient $X _ { 3 }$ Test the hypothesis $H _ { 0 } : \beta _ { 3 } = 0$ versus $H _ { 1 } : \beta _ { 3 } \neq 0 \text { at the } \alpha = 0.05$ level. What do you conclude?

• A) Reject H₀
• B) Do not reject H₀

---

Definitions:

Gross Profit Margin

A financial metric that represents the percentage of revenue that exceeds the cost of goods sold, indicating the efficiency of production.

Cost Of Goods Sold

Expenses directly associated with the creation of a company's sold products, including both materials and workforce costs.

Sales

Sales represent the total revenue earned from goods or services sold by a company during a certain period.

Gross Profit Margin

A financial ratio that indicates the percentage of revenue that exceeds the cost of goods sold, highlighting the efficiency in producing and selling products.