The Following MINITAB Output Presents a Multiple Regression Equatior $\hat { y }$

question 6

Multiple Choice

The following MINITAB output presents a multiple regression equatior $\hat { y }$ =b₀+b₁x₁+b₂x₂+b₃x₃+b₄x₄
The regression equation is
$$\mathrm { Y } = 4.7712 + 0.2662 \mathrm { X } 1 + 1.2710 \mathrm { X } 2 - 1.1349 \mathrm { X } 3 - 1.8545 \mathrm { X } 4$$
$\begin{array}{lllll}\text { Predictor } & \text { Coef } & \text { SE Coef } & \text { T } & \mathrm{P} \\\text { Constant } & 4.7712 & 0.7648 & 0.92800 & 0.3280 \\\mathrm{X} 1 & 0.2662 & 0.8036 & -0.93740 & 0.3570 \\\mathrm{X} 2 & 1.2710 & 0.8451 & 1.74170 & 0.0830 \\\mathrm{X} 3 & -1.1349 & 0.6318 & -2.94990 & 0.0080 \\\mathrm{X} 4 & -1.8545 & 0.6753 & 3.27200 & 0.0020\end{array}$



$\text { Analysis of Variance }$
$\begin{array}{lccccc}\text { Source } & \text { DF } & \text { SS } & \text { MS } & \text { F } & \text { P } \\\text { Regression } & 4 & 624.2 & 156.1 & 9.8797 & 0.003 \\\text { Residual Error } & 40 & 633.7 & 15.8 & & \\\text { Total } & 44 & 1,257.9 & & & \\\hline\end{array}$


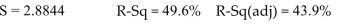
It is desired to drop one of the explanatory variables. Which of the following is the most appropriate action?

• A) Drop x₄, then see whether R² increases
• B) Drop x₁, then see whether R² increases
• C) Drop x₄, then see whether adjusted R² increases
• D) Drop x₁, then see whether adjusted R² increases

---

Definitions:

Binding Minimum Wage

A government-set minimum wage that is above the equilibrium wage, potentially leading to unemployment because the quantity of labor supplied exceeds the quantity demanded.

Labor Demanded

The total number of workers that employers are willing and able to hire at a given wage rate in a certain period of time.

Labor Supplied

The aggregate amount of hours that employees are prepared and capable of working for a specified rate of pay.

Binding Price Floor

A minimum price set by the government or body above the equilibrium price, leading to excess supply if the market cannot legally adjust to its equilibrium.