The Following MINITAB Output Presents a Multiple Regression Equation $\hat { y } = b _ { 0 } + b _ { 1 } x _ { 1 } + b _ { 2 } x _ { 2 } + b _ { 3 } x _ { 3 }$

question 31

Multiple Choice

The following MINITAB output presents a multiple regression equation $\hat { y } = b _ { 0 } + b _ { 1 } x _ { 1 } + b _ { 2 } x _ { 2 } + b _ { 3 } x _ { 3 }$ $+ b _ { 4 } x _ { 4 }$ .
The regression equation is
$$\mathrm { Y } = 1.9568 + 1.7369 \mathrm { X } 1 + 1.1099 \mathrm { X } 2 - 1.2672 \mathrm { X } 3 + 1.6080 \mathrm { X } 4$$
$\begin{array}{lllll}\text { Predictor } & \text { Coef } & \text { SE Coef } & \text { T } & \text { P } \\\text { Constant } & 1.9568 & 0.8248 & 1.1277 & 0.345 \\\text { X1 } & 1.7369 & 0.7980 & 3.4296 & 0.004 \\\text { X2 } & 1.1099 & 0.7500 & -3.2529 & 0.006 \\\text { X3 } & -1.2672 & 0.7534 & 1.8730 & 0.076 \\\text { X4 } & 1.6080 & 0.8733 & -0.9328 & 0.349\end{array}$


$\text { Analysis of Variance }$
$\begin{array}{lccccc}\text { Source } & \text { DF } & \text { SS } & \text { MS } & \text { F } & \text { P } \\\text { Regression } & 4 & 503.9 & 126.0 & 5.0806 & 0.003 \\\text { Residual Error } & 40 & 990.4 & 24.8 & & \\\text { Total } & 44 & 1,494.3 & & & \\\hline\end{array}$

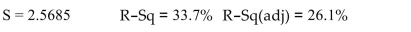
Predict the value of $\mathrm { y }$ when $x _ { 1 } = 1 , x _ { 2 } = 2 , x _ { 3 } = 3 , x _ { 4 } = 6$

• A) 9.798
• B) 9.8031
• C) 10.6228
• D) 11.7599

---

Definitions:

Favourable Variances

Differences between actual costs and budgeted costs that result in a better-than-expected financial performance, often indicating cost savings or higher revenues.

Large Variances

Significant differences between planned and actual figures in a budget, project, or any performance measurement, indicating greater deviations from expectations.

Consistent Trends

Patterns or changes in data that continue over a period of time in a similar manner.

Standard Direct Labour Hours

The estimated amount of labor hours required to produce a certain amount of output under normal conditions.