The Following MINITAB Output Presents a Multiple Regression Equatior $\hat { y }$

question 38

Multiple Choice

The following MINITAB output presents a multiple regression equatior $\hat { y }$ =b₀+b₁x₁+b₂x₂+b₃x₃+b₄x₄

The regression equation is
$$\mathrm { Y } = 2.5919 - 1.3391 \mathrm { X } 1 + 0.6212 \mathrm { X } 2 + 1.6435 \mathrm { X } 3 + 1.4269 \mathrm { X } 4$$

$\begin{array}{lllll}\text { Predictor } & \text { Coef } & \text { SE Coef } & \text { T } & \text { P } \\\text { Constant } & 2.5919 & 0.6269 & 1.1668 & 0.337 \\\text { X1 } & -1.3391 & 0.6716 & 3.5190 & 0.002 \\\text { X2 } & 0.6212 & 0.8488 & -3.2848 & 0.004 \\\text { X3 } & 1.6435 & 0.7934 & 1.8821 & 0.090 \\\text { X4 } & 1.4269 & 0.7679 & -0.9879 & 0.345\end{array}$




$\text { Analysis of Variance }$
$\begin{array}{lccccc}\text { Source } & \text { DF } & \text { SS } & \text { MS } & \text { F } & \text { P } \\\text { Regression } & 4 & 735.9 & 184.0 & 7.7311 & 0.003 \\\text { Residual Error } & 25 & 594.6 & 23.8 & & \\\text { Total } & 29 & 1,330.5 & & & \\\hline\end{array}$
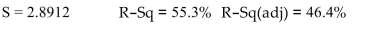
Let $\beta _ { 3 }$ be the coefficient $X _ { 3 }$ Test the hypothesis $H _ { 0 } : \beta _ { 3 } = 0$ versus $H _ { 1 } : \beta _ { 3 } \neq 0 \text { at the } \alpha = 0.05$ level. What do you conclude?

• A) Reject H₀
• B) Do not reject H₀

---

Definitions:

Loan

Borrowed funds that must be repaid with interest, used by individuals or entities to finance various activities.