The Following MINITAB Output Presents a Multiple Regression Equatior $\hat { y }$

question 6

Multiple Choice

The following MINITAB output presents a multiple regression equatior $\hat { y }$ =b₀+b₁x₁+b₂x₂+b₃x₃+b₄x₄
The regression equation is
$$\mathrm { Y } = 4.7712 + 0.2662 \mathrm { X } 1 + 1.2710 \mathrm { X } 2 - 1.1349 \mathrm { X } 3 - 1.8545 \mathrm { X } 4$$
$\begin{array}{lllll}\text { Predictor } & \text { Coef } & \text { SE Coef } & \text { T } & \mathrm{P} \\\text { Constant } & 4.7712 & 0.7648 & 0.92800 & 0.3280 \\\mathrm{X} 1 & 0.2662 & 0.8036 & -0.93740 & 0.3570 \\\mathrm{X} 2 & 1.2710 & 0.8451 & 1.74170 & 0.0830 \\\mathrm{X} 3 & -1.1349 & 0.6318 & -2.94990 & 0.0080 \\\mathrm{X} 4 & -1.8545 & 0.6753 & 3.27200 & 0.0020\end{array}$



$\text { Analysis of Variance }$
$\begin{array}{lccccc}\text { Source } & \text { DF } & \text { SS } & \text { MS } & \text { F } & \text { P } \\\text { Regression } & 4 & 624.2 & 156.1 & 9.8797 & 0.003 \\\text { Residual Error } & 40 & 633.7 & 15.8 & & \\\text { Total } & 44 & 1,257.9 & & & \\\hline\end{array}$


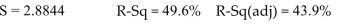
It is desired to drop one of the explanatory variables. Which of the following is the most appropriate action?

• A) Drop x₄, then see whether R² increases
• B) Drop x₁, then see whether R² increases
• C) Drop x₄, then see whether adjusted R² increases
• D) Drop x₁, then see whether adjusted R² increases

---

Definitions:

Permanent Account

An account that carries its ending balance over to the next accounting period, typically representing real accounts like assets, liabilities, and equity.

Closing Process

The steps taken at the end of an accounting period to prepare accounts for the next period, including zeroing out temporary accounts.

Closing the Books

Closing the books is an accounting process involving updating ledger accounts at the end of an accounting period to prepare financial statements.

Fiscal Year

A twelve-month period used for accounting purposes to prepare financial statements, which may or may not align with the calendar year.