
-Provide missing statements and missing reasons for the following proof.
Given: 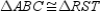 ; M is the midpoint of
; M is the midpoint of 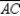 and N is the midpoint of
and N is the midpoint of  Prove:
Prove: 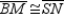 S1.
S1. 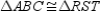 R1.
R1.
S2. 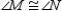 ,
,  , and
, and 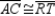 R2.
R2.
S3. R3. Given
S4.  R4. The midpoints of two congruent line segments
R4. The midpoints of two congruent line segments
divide the segments into 4 congruent segments.
S5.  R5.
R5.
S6. R6.
Definitions:
Mean
The mean of a collection of numbers, found by dividing their total sum by the quantity of numbers in the set.
μ
The symbol commonly used to represent the mean or average of a population in statistics.
σ
Represents the standard deviation of a population in statistics, measuring the dispersion of dataset values from the mean.
Normally Distributed
Refers to a probability distribution that is even on both sides of its mean, indicating that values close to the mean happen more often than values far from the mean.
Q1: A child is brought to the clinic
Q3: The parent of a child diagnosed with
Q5: Given the rhombus RSTV, diagonals <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7237/.jpg"
Q6: Because of their inability to ambulate, children
Q23: A preschoolage child is brought to clinic
Q212: According to the Distance Formula, the distance
Q374: A diagonal of a parallelogram separates the
Q420: If the diagonals of a rhombus have
Q614: In <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7237/.jpg" alt="In ,
Q911: To show analytically that two lines are