Suppose a Country's Population at Any Time T Grows in Accordance

question 12

Short Answer

Suppose a country's population at any time t grows in accordance with the rule ​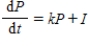 where P denotes the population at any time t, k is a positive constant reflecting the natural growth rate of the population, and I is a constant giving the (constant) rate of immigration into the country. The population of the United States in the year 1980 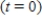was 224.5 million. Suppose the natural growth rate is 0.8% annually 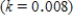and net immigration is allowed at the rate of 0.5 million people/year 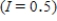until the end of the century. What will be the U.S. population in 2003? Round the answer to the nearest tenth of a million, if necessary. P=__________ million

---

Definitions:

Time-Series Analysis

A statistical method used to examine and interpret a sequence of data points, collected over a period of time, to identify trends or patterns.

Return On Equity

A measure of a corporation's profitability that reveals how much profit a company generates with the money shareholders have invested.

Du Pont Model

The Du Pont Model is a framework for analyzing a company's return on equity (ROE) by breaking it down into three components: profit margin, asset turnover, and financial leverage.

Net Profit Margin

A profitability metric indicating the percentage of revenue left as net income after all expenses, taxes, and costs have been subtracted.