Show That the Function 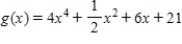Is Concave Upward Wherever It

question 14

Multiple Choice

Show that the function is concave upward wherever it is defined. ​

• A) The function is defined for any value of x and hence the function is concave upward for any x.
• B) The second derivative of is . It is positive for any value of x, hence the function is concave upward for any x.
• C) The first derivative of is . It is positive for any value of x, hence the function is concave upward for any x.

---

Definitions:

Channel Functions

Activities involved in moving goods from producers to consumers, including distribution, transportation, and retailing.

Rack Jobbers

Merchandisers who lease space within retail stores to display and sell their own products, typically involved in the distribution of books, music, or electronics.

Consignment

A sales arrangement where goods are left with a third party to sell, but ownership remains with the supplier until sold.

Merchant Wholesalers

Businesses that buy goods in large quantities from producers to resell to retailers or other businesses, but not to end consumers.