TABLE 10-9 The Following Excel Output Contains the Results of a Test

question 27

Multiple Choice

TABLE 10-9
The following Excel output contains the results of a test to determine whether the proportions of satisfied customers at two resorts are the same or different.

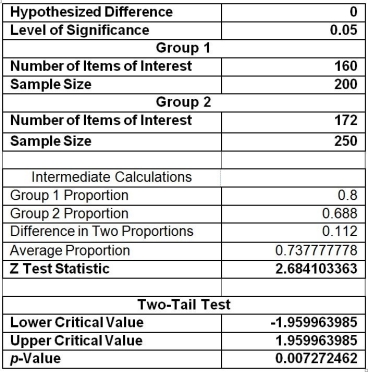
-Referring to Table 10-9, allowing for 1% probability of committing a Type I error, what are the decision and conclusion on testing whether there is any difference in the proportions of satisfied customers in the two resorts?

• A) Do not reject the null hypothesis; there is enough evidence to conclude that there is significant difference in the proportions of satisfied guests at the two resorts.
• B) Do not reject the null hypothesis; there is not enough evidence to conclude that there is significant difference in the proportions of satisfied guests at the two resorts.
• C) Reject the null hypothesis; there is enough evidence to conclude that there is significant difference in the proportions of satisfied guests at the two resorts.
• D) Reject the null hypothesis; there is not enough evidence to conclude that there is significant difference in the proportions of satisfied guests at the two resorts.

---

Definitions:

Bromides

Commonplace remarks or clichés that lack originality or interest.

Platitudes

Overused statements or cliches that often lack originality or significance.

Pareto Efficient Allocation

A situation in economic theory where resources are allocated in such a way that it is impossible to make any one individual better off without making at least one individual worse off.

Pareto Optimal Allocation

A resource distribution scenario where no individual can be made better off without making at least one individual worse off.