TABLE 14-15 the Superintendent of a School District Wanted to Predict the Predict

question 317

True/False

TABLE 14-15
The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test. She obtained the data on percentage of students passing the proficiency test (% Passing), daily mean of the percentage of students attending class (% Attendance), mean teacher salary in dollars (Salaries), and instructional spending per pupil in dollars (Spending) of 47 schools in the state.
Following is the multiple regression output with Y = % Passing as the dependent variable, X₁ = % Attendance, X₂= Salaries and X₃= Spending:

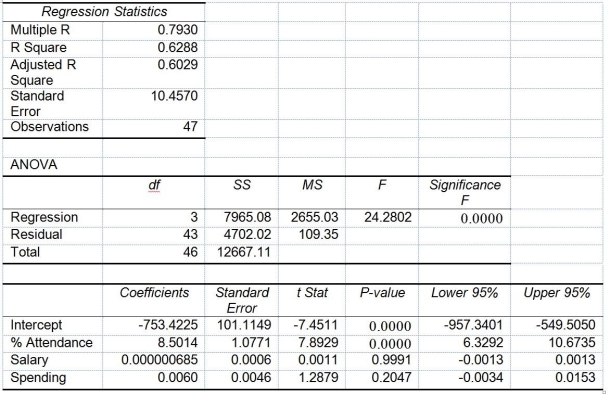
-Referring to Table 14-15, you can conclude that instructional spending per pupil individually has no impact on the mean percentage of students passing the proficiency test, taking into account the effect of all the other independent variables, at a 10% level of significance based solely on the 95% confidence interval estimate for β₃.

---

Definitions:

Population Proportion

The fraction or percentage of a population that exhibits a particular trait or characteristic.

Confidence Interval

A range of values, derived from sample statistics, that is likely to contain the value of an unknown population parameter at a given confidence level.

Population Proportion

The fraction of the population that possesses a particular attribute, characteristic, or trait.

Standard Normal Distribution

A probability distribution that has a mean of zero and a standard deviation of one, used in statistical analysis to represent standardized values of a dataset.