Examlex

Solved

If We Want to Relate a Random Variable Y to Two-Independent

question 16

True/False

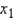If we want to relate a random variable y to two-independent variables If we want to relate a random variable y to two-independent variables and , a regression hyperplane is the three-dimensional equivalent of a regression line that minimizes the sum of the squared vertical deviations between the sample points suspended in y vs. vs. space and their associated multiple regression estimates, all of which lie on this hyperplane. 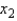and If we want to relate a random variable y to two-independent variables and , a regression hyperplane is the three-dimensional equivalent of a regression line that minimizes the sum of the squared vertical deviations between the sample points suspended in y vs. vs. space and their associated multiple regression estimates, all of which lie on this hyperplane. , a regression hyperplane is the three-dimensional equivalent of a regression line that minimizes the sum of the squared vertical deviations between the sample points suspended in y vs. 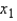If we want to relate a random variable y to two-independent variables and , a regression hyperplane is the three-dimensional equivalent of a regression line that minimizes the sum of the squared vertical deviations between the sample points suspended in y vs. vs. space and their associated multiple regression estimates, all of which lie on this hyperplane. vs. 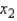If we want to relate a random variable y to two-independent variables and , a regression hyperplane is the three-dimensional equivalent of a regression line that minimizes the sum of the squared vertical deviations between the sample points suspended in y vs. vs. space and their associated multiple regression estimates, all of which lie on this hyperplane. space and their associated multiple regression estimates, all of which lie on this hyperplane.

Definitions:

Related Questions

Q9: To be valid, the chi-square test requires

Q22: Americans are very vocal about their

Q27: Which one of the following statements correctly

Q29: The ideology of individual members of Congress

Q56: About _ % of states allow citizen-generated

Q98: Apply the Friedman test to the accompany

Q105: The rank correlation coefficient is used when

Q123: The width of the confidence interval estimate

Q139: In the randomized block design ANOVA, the

Q140: The analysis of variance, ANOVA, is best