In Testing Whether the Means of Two Normal Populations Are

question 205

Multiple Choice

In testing whether the means of two normal populations are equal, summary statistics computed for two independent samples are as follows: 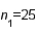, , 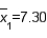, , 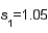, 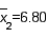and 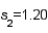. Assume that the population variances are equal. Then, the standard error of the sampling distribution of the sample mean difference 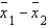is equal to:

• A) 0.1017
• B) 1.2713
• C) 0.3189
• D) 1.1275
• E) 0.4812

---

Definitions:

Spearman Rank

A nonparametric measure of rank correlation that assesses how well the relationship between two variables can be described using a monotonic function.

Ordinal Variables

Variables that represent categories with a natural order or ranking among them, though the intervals between the rankings may not be equal.

Interval Variables

Variables that have measurable distances between values but no true zero point, allowing for the calculation of meaningful differences.

Relationship

A connection or association between two or more variables in a dataset or study.