Let 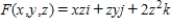and Let S Be the Surface Bounded by

question 59

Multiple Choice

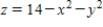Let and let S be the surface bounded by and 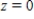. Verify the Divergence Theorem by evaluating as a surface integral and as a triple integral. Round your answer to two decimal places.
​

---

Definitions:

Binomial

A type of probability distribution with two possible outcomes, used to model situations with fixed numbers of trials and the same probability of success.

Population Proportions

The ratio of members in a statistical population who have a particular attribute, compared to the total number of members in the population.

Pooled Proportion Estimate

An estimation technique that combines the proportions of two or more groups into a single overall proportion.

Sample 1

A subset of individuals or items selected from a larger population for the purpose of statistical analysis.