Solve the Problem $\mathrm { f } _ { 1 } ( \mathrm { x } ) = - \mathrm { x } ^ { 2 } + 100 \mathrm { x } ; \mathrm { f } _ { 2 } ( \mathrm { x } ) = 85 \mathrm { x }$

question 205

Multiple Choice

Solve the problem.
-The following information pertains to a bakery which makes donuts.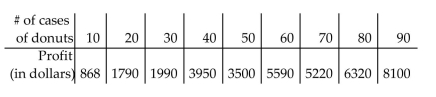


Make a scatterplot of the data. Then graph the following two functions on the same coordinate system: $\mathrm { f } _ { 1 } ( \mathrm { x } ) = - \mathrm { x } ^ { 2 } + 100 \mathrm { x } ; \mathrm { f } _ { 2 } ( \mathrm { x } ) = 85 \mathrm { x }$ . Decide which function best models the data, and then use that function to estimate the profit associated with making 35 cases of donuts.

• A) \(\mathrm { f } _ { 2 }\); Profit for 35 cases is \(\$ 2975\).
• B) \(\mathrm { f } _ { 1 }\); Profit for 35 cases is \(\$ 2275\).
• C) \(\mathrm { f } _ { 1 }\); Profit for 35 cases is \(\$ 2625\).
• D) \(\mathrm { f } _ { 2 }\); Profit for 35 cases is \(\$ 3525 .\)

---

Definitions:

Infrastructure Assets

Long-term physical assets that are critical for providing public services, including roads, bridges, and water supply systems.

Maintenance Costs

Expenses incurred to keep an asset in working order or restore it to proper condition; does not improve upon the original asset.

Government-Wide Financial Statements

Comprehensive reports that provide an overview of a government entity’s financial activities and balances, including both governmental and business-type activities.

Rare Painting

Describes a unique or scarce artwork that is often highly valued due to its rarity, artist, historical significance, or aesthetics.