TABLE 13-15
The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test. She obtained the data on percentage of students passing the proficiency test (% Passing) , daily mean of the percentage of students attending class (% Attendance) , mean teacher salary in dollars (Salaries) , and instructional spending per pupil in dollars (Spending) of 47 schools in the state.
Following is the multiple regression output with Y = % Passing as the dependent variable, 
= : % Attendance,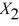 
= Salaries and 
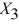= Spending:
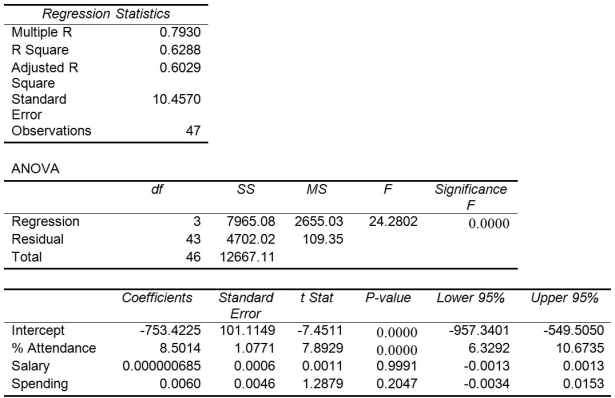
-Referring to Table 13-15, which of the following is a correct statement?
Definitions:
Capital Budgeting Process
The procedure businesses follow to evaluate potential major projects or investments, through stages from proposal generation to project approval.
Favorably Biased
A tendency to present information in a manner that is more positive or beneficial than is justified by the facts.
Annual Depreciation Expense
The portion of the cost of a fixed asset that is expensed each year of its useful life, representing wear and tear, decay, or decrease in value.
Cash Inflows
Refers to the money received by a business from its operational, investment, and financing activities.
Q4: Referring to Table 13-17 Model 1, which
Q44: With _ arrangements,temporary employees generally do not
Q51: A regression had the following results: SST
Q56: Referring to Table 13-11, in terms of
Q88: Referring to Table 11-5, the value of
Q100: One of the morals of the red
Q107: Referring to Table 12-2, what percentage of
Q116: Referring to Table 12-13, the conclusion on
Q193: Referring to Table 13-17 Model 1, which
Q276: Referring to Table 13-4, at the 0.01