The Parametric Equations for the Path of a Projectile Launched $\theta$

question 95

Multiple Choice

The parametric equations for the path of a projectile launched at a height h feet above the ground, at an angle $\theta$ with the horizontal and having an initial velocity of $v _ { 0 }$ feet per second is given by $x = \left( v _ { 0 } \cos \theta \right) t$ and $y = h + \left( v _ { 0 } \sin \theta \right) t - 16 t ^ { 2 }$ . The center field fence in a ballpark is 10 feet high and 400 feet from home plate. The ball is hit 3 feet above the ground. It leaves the bat at an angle of $\theta$ degrees with the horizontal at a speed of 100 miles per hour as shown in the figure. Find the minimum angle at which the ball must leave the bat in order for the hit to be a home run using the parametric equations $x = \left( \frac { 440 } { 3 } \cos \theta \right) t$ and $y = 3 + \left( \frac { 440 } { 3 } \sin \theta \right) t - 16 t ^ { 2 }$ . Round your answer to one decimal place.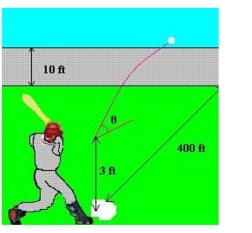

• A) \(25.5 ^ { \circ }\)
• B) \(19.4 ^ { \circ }\)
• C) \(3.4 ^ { \circ }\)
• D) \(4.5 ^ { \circ }\)
• E) \(11.3 ^ { \circ }\)

---

Definitions:

Normally Distributed

This describes a probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean.

Average Balance

The mean value derived from summing all balances over a certain period and dividing by the number of periods.

Standard Deviation

A gauge for the level of variance or scattering of values within a dataset.

Exponential Distribution

A continuous probability distribution used to model the time between events in a process where events occur continuously and independently at a constant average rate.