Multiple Choice
Verify the Divergence Theorem by evaluating as a surface integral and as a triple integral.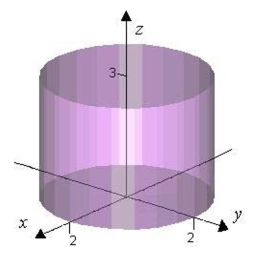
Definitions:
Related Questions
Q4: If the futures price falls,<br>1) the short
Q24: Find the general solution of the
Q26: If an option has no intrinsic value,
Q29: Small margin requirements for futures contracts implies<br>1)
Q46: Evaluate the following iterated integral. <br>
Q53: Find an equation in rectangular coordinates
Q67: A baseball is hit 3 feet
Q69: Find a set of parametric
Q85: Find the first partial derivative for
Q112: Find the Jacobian for the change