Find the Particular Solution of the Differential Equation $\frac { w } { g } y ^ { tt } ( t ) + b y ^ { t } ( t ) + k y ( t ) = \frac { w } { g } F ( t )$

question 28

Multiple Choice

Find the particular solution of the differential equation $\frac { w } { g } y ^ { tt } ( t ) + b y ^ { t } ( t ) + k y ( t ) = \frac { w } { g } F ( t )$ for the oscillating motion of an object on the end of a spring. In the equation, $y$ is the displacement from equilibrium (positive direction is downward) measured in feet, and $t$ is the time in seconds (see figure) . The constant $w = 4$ is the weight of the object, $g = 32$ is the acceleration due to gravity, $b = \frac { 1 } { 2 }$ is the magnitude of the resistance to the motion, $k = \frac { 25 } { 2 }$ is the spring constant from Hooke's Law, $F ( t ) = 4 \sin 8 t$ is the acceleration imposed on the system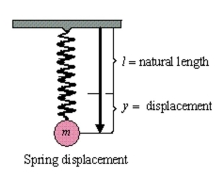, $y ( 0 ) = \frac { 1 } { 5 }$ and $y ^ { t } ( 0 ) = - 6$

• A) \(y = \frac { 37 } { 145 } e ^ { - 2 t } \cos ( 4 \sqrt { 6 } t ) + \frac { 217 \sqrt { 6 } } { 870 } e ^ { - 2 t } \sin ( 4 \sqrt { 6 } t ) + \frac { 9 } { 145 } \sin 8 t - \frac { 8 } { 145 } \cos 8 t\)
• B) \(y = \frac { 1 } { 5 } e ^ { 2 t } \sin ( 3 \sqrt { 6 } t ) + \frac { 7 \sqrt { 6 } } { 30 } e ^ { 2 t } \cos ( 3 \sqrt { 6 } t ) + \frac { 7 } { 145 } \sin 8 t + \frac { 8 } { 145 } \cos 8 t\)
• C) \(y = \frac { 37 } { 145 } e ^ { - 2 t } \sin ( 2 \sqrt { 5 } t ) + \frac { 7 \sqrt { 3 } } { 30 } e ^ { - 2 t } \cos ( 2 \sqrt { 5 } t ) - \frac { 9 } { 145 } \sin 8 t - \frac { 7 } { 145 } \cos 8 t\)
• D) \(y = \frac { 1 } { 5 } e ^ { - 2 t } \cos ( 8 \sqrt { 2 } t ) - \frac { 217 \sqrt { 6 } } { 870 } e ^ { - 2 t } \sin ( 8 \sqrt { 2 } t ) + \frac { 8 } { 145 } \sin 8 t - \frac { 9 } { 145 } \cos 8 t\)
• E)\(y = \frac { 1 } { 5 } e ^ { 2 t } \cos ( 7 \sqrt { 3 } t ) - \frac { 7 \sqrt { 3 } } { 30 } e ^ { 2 t } \sin ( 7 \sqrt { 3 } t ) + \frac { 9 } { 145 } \sin 8 t - \frac { 7 } { 145 } \cos 8 t\)

---

Definitions:

Methyl Isobutyrate

An organic compound with the formula C5H10O2, used as a flavoring agent and solvent.

Acid Chloride

Organic compounds belonging to the acyl chloride group, characterized by a carbon-oxygen double bond connected to a chlorine atom, used as intermediates in organic synthesis.

2° Amine

A type of amine where the nitrogen atom is attached to two alkyl or aryl groups and one hydrogen atom.

Compound

A compound is a substance formed when two or more chemical elements are chemically bonded together.