Find the Dimensions of the Rectangle Enclosed in the Semicircle $y = \sqrt { 144 - x ^ { 2 } }$

question 67

Multiple Choice

Find the dimensions of the rectangle enclosed in the semicircle $y = \sqrt { 144 - x ^ { 2 } }$ with the largest possible area.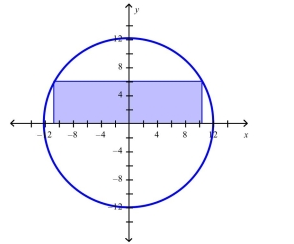

• A) 5 in. \(\times 7\) in.
• B) 6 in. \(\times 6\) in.
• C) \(12 \sqrt { 2 }\) in. \(\times 6 \sqrt { 2 }\) in.
• D) \(6 \sqrt { 2 }\) in. \(\times 6 \sqrt { 2 }\) in.

---

Definitions:

Exponential Service

A distribution model describing the time between events in a Poisson process, often used in queuing theory to model times between services.

Poisson Arrival

Describes a process where events occur randomly and independently of one another at a constant average rate, often used in queueing theory.

Waiting Line System

A methodical process used to manage the queue of entities waiting to receive services, optimizing both service and waiting times.

Available Teller

Refers to a bank employee who is present and able to assist customers with transactions and inquiries.