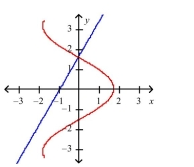
Two Curves Are Said to Be Orthogonal If Their Tangent $$y - \frac { 7 } { 4 } x = \frac { \pi } { 2 } , \quad x = \frac { 7 } { 4 } \cos y$$

question 38

Short Answer

Two curves are said to be orthogonal if their tangent lines are perpendicular at each point of intersection of the curves. Show that the curves of the given equations are orthogonal.
$$y - \frac { 7 } { 4 } x = \frac { \pi } { 2 } , \quad x = \frac { 7 } { 4 } \cos y$$

---

Definitions:

Sterile Drape

A sterile covering used in medical procedures to maintain a sterile field by isolating the operative area from possible contaminants.

Surgical Asepsis

Techniques used to maintain a sterile environment in order to prevent infection during surgical procedures.

Medical Asepsis

Practices aimed at reducing the number and spread of pathogens to prevent infection.

Mayo Stand

A stainless steel removable instrument tray set on a movable stand that is positioned over or adjacent to a surgical site; it provides a place for sterile instruments and supplies used during surgery.