Life Without Their Physical Capture and Handling Defined as the Number of Captures Per 100 Trap-Nights
life without their physical capture and handling. In a recent study of
bobcat (Lynx rufus) abundance, camera traps were placed at varying
distances from a road. The data on trapping success from 8 trapping
stations are presented in the table at right. The trapping success is
Remote camera trapping is used to detect and monitor elusive wild- defined as the number of captures per 100 trap-nights.
-Hemorrhagic disease in white-tailed deer is caused by a virus known as EHD.
Immunity is given to fawns by transfer of EHD antibodies from the mother. In a
study to determine how long the maternal antibodies last, blood samples were taken
from a large sample of fawns of varying ages. The mean levels of EHD antibody
concentration and the associated ages of fawns are given in the table below.
After using the data to fit a straight line model, Eˆ = a + bW , significant curvature was
detected in the residual plot. Two nonlinear models were chosen for further analysis,
the exponential and the power models. (For these data, common logs were used to
perform the transformations.) The computer output for these models is given below,
and the residual plots are on the next page.
(Exponential)
Bivariate Fit of LogE By Age
Age
Summary of Fit
(Power)
Bivariate Fit of LogE By LogAge
LogAge
Summary of Fit
Fawn data
Residual Plots
Residual Plot - Exponential Model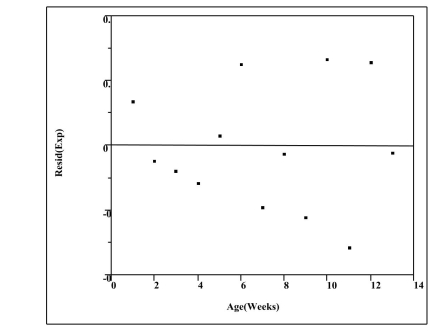
Residual Plot - Power Model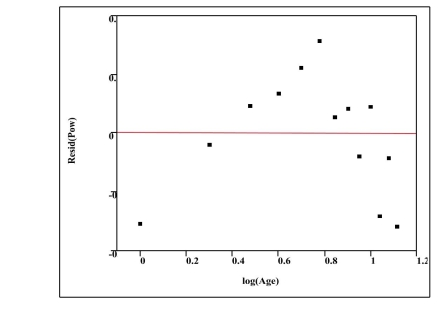
a) For the exponential model, calculate the predicted logarithm of the EHD antibody
concentration for an age of 5 weeks.
b) Generally speaking, which of the two models, power or exponential, is a better
choice for predicting the logarithm of the EHD antibody concentration? Provide
statistical justification for your choice based on both the residual plot and the
numerical summary statistics above.
c) The researchers want use their model to predict EHD antibody concentrations for
fawns up to 24 weeks of age. Do you think this would be reasonable? Explain
why or why not.
Definitions:
Statement Of Owner's Equity
A financial statement detailing changes in the equity of a company's owner over a reporting period.
Capital Changes
Adjustments or alterations in the equity or ownership capital of a company, often due to investments, dividends, or profits.
Accounting Period
A specific period of time for which financial activities are recorded and reported, such as a month, quarter, or year.
Withdrawals
Withdrawals indicate the amount of money or assets taken out from a business by its owner(s) for personal use.
Q4: By definition, a data point is an
Q10: <span class="ql-formula" data-value="\bar { x } \text
Q23: T The foraging capability of Downy
Q28: The standard error of <span
Q38: The Addition Rule states that for
Q56: Solve the initial-value problem.<br> <span class="ql-formula"
Q93: The very poorest low-income DVCs typically have
Q112: A recommended policy for DVCs to implement
Q179: Population growth remains high in most DVCs<br>A)
Q226: In the DVCs, underemployment frequently takes the