Life Without Their Physical Capture and Handling Defined as the Number of Captures Per 100 Trap-Nights

question 11

Essay

life without their physical capture and handling. In a recent study of
bobcat (Lynx rufus) abundance, camera traps were placed at varying
distances from a road. The data on trapping success from 8 trapping
stations are presented in the table at right. The trapping success is
Remote camera trapping is used to detect and monitor elusive wild- $$\begin{array} { | r | r | } \hline \begin{array} { c } \text { Distance } \\\text { (m) }\end{array} & \begin{array} { c } \text { Trap } \\\text { Success }\end{array} \\\hline 115 & 2.0 \\\hline 326 & 1.6 \\\hline 528 & 2.0 \\\hline 979 & 1.7 \\\hline 1252 & 1.9 \\\hline 1252 & 4.6 \\\hline 1459 & 5.7 \\\hline 2145 & 5.4 \\\hline\end{array}$$ defined as the number of captures per 100 trap-nights.
-Hemorrhagic disease in white-tailed deer is caused by a virus known as EHD.
Immunity is given to fawns by transfer of EHD antibodies from the mother. In a
study to determine how long the maternal antibodies last, blood samples were taken
from a large sample of fawns of varying ages. The mean levels of EHD antibody
concentration and the associated ages of fawns are given in the table below.
After using the data to fit a straight line model, Eˆ = a + bW , significant curvature was
detected in the residual plot. Two nonlinear models were chosen for further analysis,
the exponential and the power models. (For these data, common logs were used to
perform the transformations.) The computer output for these models is given below,
and the residual plots are on the next page. $$\widehat{\log E}=a+b W$$
(Exponential)
Bivariate Fit of LogE By Age
$\log E=1.694-0.076$ Age
Summary of Fit
$\begin{array}{|l|r|}\hline \text { RSquare } & 0.975 \\\hline \text { RSquare Adj } & 0.973 \\\hline \text { St. Dev. Of Residuals } & 0.049 \\\hline\end{array}$
$$\widehat{\log E}=a+b \log W$$
(Power)
Bivariate Fit of LogE By LogAge
$\log E=1.694-0.076$ LogAge
Summary of Fit
$\begin{array}{|l|l|}\hline \text { RSquare } & 0.889 \\\hline \text { RSquare Adj } & 0.879 \\\hline \text { St. Dev. Of Residuals } & 0.105 \\\hline\end{array}$
Fawn data
$\begin{array}{|c|c|}\hline \begin{array}{l}\text { W=Age } \\\text { (Weeks) }\end{array} & \begin{array}{l}\text { E=Mean } \\\text { EHDV } \\\text { Conc. }\end{array} \\\hline 1 & 45 \\\hline 2 & 34 \\\hline 3 & 28 \\\hline 4 & 23 \\\hline 5 & 21 \\\hline 6 & 20 \\\hline 7 & 13 \\\hline 8 & 12 \\\hline 9 & 9 \\\hline 10 & 10 \\\hline 11 & 6 \\\hline 12 & 7 \\\hline 13 & 5 \\\hline\end{array}$ Residual Plots
$$\widehat { \log E } = a + b W$$
Residual Plot - Exponential Model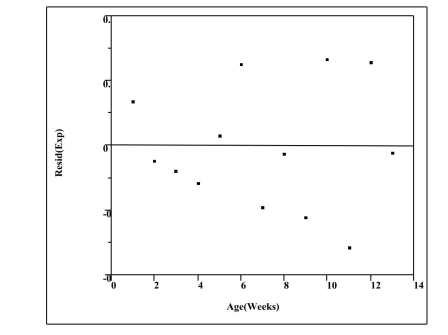


$$\widehat { \log E } = a + b \log W$$
Residual Plot - Power Model

a) For the exponential model, calculate the predicted logarithm of the EHD antibody
concentration for an age of 5 weeks.
b) Generally speaking, which of the two models, power or exponential, is a better
choice for predicting the logarithm of the EHD antibody concentration? Provide
statistical justification for your choice based on both the residual plot and the
numerical summary statistics above.
c) The researchers want use their model to predict EHD antibody concentrations for
fawns up to 24 weeks of age. Do you think this would be reasonable? Explain
why or why not.

---

Definitions:

Internet During Class

The use of the internet by students for non-educational purposes during class times, which can be a distraction and hinder learning.

Research Results

The findings or outcomes derived from systematic investigation aimed at discovering new knowledge or understanding.

Taking Notes

The act of writing down important information from a verbal instruction, lecture, or reading material for future reference.

Long-term Storage

The process and capability of retaining information in the brain or a digital device for extended periods of time.