The Circuit Shown Below, Let (A) Write a Node Equation at Node 1 by Summing

question 5

Essay

the circuit shown below, let $\mathrm { R } _ { 1 } = 1 \mathrm { k } \Omega , \mathrm { R } _ { 2 } = 4 \mathrm { k } \Omega , \mathrm { R } _ { \mathrm { i } } = 3 \mathrm { k } \Omega , \mathrm { R } _ { \mathrm { o } } = 2 \mathrm { k } \Omega , \mathrm { A } = 1000 , \mathrm { v } _ { \mathrm { s } } = 1 \mathrm {~V} , \mathrm { v } _ { \mathrm { p } } = \mathrm { v } _ { \mathrm { s } }$
(a) Write a node equation at node 1 by summing currents away from node 1 .
(b) Write a node equation at node 2 by summing currents away from node 2 .
(c) Solve the two node equations to find numerical values of $v _ { n }$ and $v _ { o }$ .
(d) Find the value of $i _ { s }$ through $R _ { i }$ . Find the input impedance 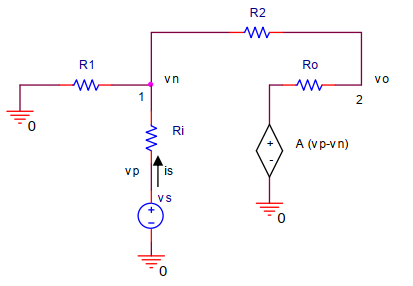$R _ { i n } = v _ { s } / i _ { s }$ .

---

Definitions:

Median

The middle value in a data set, which divides the set into two equal halves.

Outliers

Data points that differ significantly from other observations, possibly indicating variability or error in the data.

Wages

Compensation received by employees for their labor or services, typically on an hourly, daily, or piecework basis.

Skewed

A distribution that is not symmetric and has one tail longer than the other, indicating that the data are not evenly distributed around the mean.