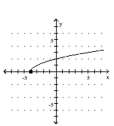
For the Given Function, Find the Domain and Range of Both

question 155

Multiple Choice

For the given function, find the domain and range of both f(x) and ${ f } ^ { - 1 } ( \mathrm { x } ) .$
-

• A) \(\begin{array} { l } \mathrm { f } : \quad \text { domain: } \{ x \mid x \geq - 4 \} \\ ~~~~\text { range: } \{ \mathrm { y } \mid \mathrm { y } \geq 0 \} \\ \mathrm { f } ^ { - 1 } : \text { domain: } \{ x \mid \mathrm { x } \geq - 4 \} \\ ~~~~\text { range: } \{ \mathrm { y } \mid \mathrm { y } \geq 0 \} \end{array}\)
• B) f: domain: \(\{ x \mid x \geq - 4 \}\) \(~~~~\)range: \(\{ y \mid y \geq 0 \}\) \(\mathrm { f } ^ { - 1 }\) : domain: \(\{ \mathrm { x } \mid \mathrm { x } \geq 0 \}\) \(~~~~\)range: \(\{ y \mid y \geq - 4 \}\)
• C) f: domain: \(\{ x \mid x \geq 0 \}\) \(~~~~\)range: \(\{ y \mid y \geq - 4 \}\) \(\mathrm { f } ^ { - 1 }\) : domain: \(\{ x \mid \mathrm { x } \geq - 4 \}\) \(~~~~\)range: \(\{ y \mid y \geq 0 \}\)
• D) f: domain: \(\{ x \mid x \geq 0 \}\) \(~~~~\)range: \(\{ y \mid y \geq - 4 \}\) \(\mathrm { f } ^ { - 1 }\) : domain: \(\{ \mathrm { x } \mid \mathrm { x } \geq 0 \}\) \(~~~~\)range: \(\{ y \mid y \geq - 4 \}\)

---

Definitions:

Elder Abuse

Any form of mistreatment that results in harm or loss to an older person, including physical, emotional, sexual abuse, neglect, and financial exploitation.

Powerless

Lacking the ability, strength, or capacity to act, influence, or assert control over circumstances or other individuals, often due to social, political, or economic constraints.

Boomerang Kid

An adult who returns to live with their parents after a period of independence, often due to economic or personal reasons.

Marital Satisfaction

The feeling of contentment and fulfillment experienced by partners within a marital relationship.