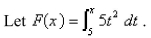Examlex

Solved

AUse Part 1 of the Fundamental Theorem of Calculus to Find

question 9

Essay

a.Use Part 1 of the Fundamental Theorem of Calculus to find b.Use Part 2 of the Fundamental Theorem of Calculus to integrate to obtain an alternative expression for c.Differentiate the expression for found in part (b).The Fundamental Theorem of Calculus, Part 1 If is continuous on [ then the function defined by is differentiable on and The Fundamental Theorem of Calculus, Part 2 If is continuous on then where is any antiderivative of that is, a.Use Part 1 of the Fundamental Theorem of Calculus to find a.Use Part 1 of the Fundamental Theorem of Calculus to find b.Use Part 2 of the Fundamental Theorem of Calculus to integrate to obtain an alternative expression for c.Differentiate the expression for found in part (b).The Fundamental Theorem of Calculus, Part 1 If is continuous on [ then the function defined by is differentiable on and The Fundamental Theorem of Calculus, Part 2 If is continuous on then where is any antiderivative of that is, b.Use Part 2 of the Fundamental Theorem of Calculus to integrate a.Use Part 1 of the Fundamental Theorem of Calculus to find b.Use Part 2 of the Fundamental Theorem of Calculus to integrate to obtain an alternative expression for c.Differentiate the expression for found in part (b).The Fundamental Theorem of Calculus, Part 1 If is continuous on [ then the function defined by is differentiable on and The Fundamental Theorem of Calculus, Part 2 If is continuous on then where is any antiderivative of that is, to obtain an alternative expression for a.Use Part 1 of the Fundamental Theorem of Calculus to find b.Use Part 2 of the Fundamental Theorem of Calculus to integrate to obtain an alternative expression for c.Differentiate the expression for found in part (b).The Fundamental Theorem of Calculus, Part 1 If is continuous on [ then the function defined by is differentiable on and The Fundamental Theorem of Calculus, Part 2 If is continuous on then where is any antiderivative of that is, c.Differentiate the expression for a.Use Part 1 of the Fundamental Theorem of Calculus to find b.Use Part 2 of the Fundamental Theorem of Calculus to integrate to obtain an alternative expression for c.Differentiate the expression for found in part (b).The Fundamental Theorem of Calculus, Part 1 If is continuous on [ then the function defined by is differentiable on and The Fundamental Theorem of Calculus, Part 2 If is continuous on then where is any antiderivative of that is, found in part (b).The Fundamental Theorem of Calculus, Part 1 If 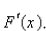a.Use Part 1 of the Fundamental Theorem of Calculus to find b.Use Part 2 of the Fundamental Theorem of Calculus to integrate to obtain an alternative expression for c.Differentiate the expression for found in part (b).The Fundamental Theorem of Calculus, Part 1 If is continuous on [ then the function defined by is differentiable on and The Fundamental Theorem of Calculus, Part 2 If is continuous on then where is any antiderivative of that is, is continuous on [ 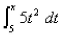a.Use Part 1 of the Fundamental Theorem of Calculus to find b.Use Part 2 of the Fundamental Theorem of Calculus to integrate to obtain an alternative expression for c.Differentiate the expression for found in part (b).The Fundamental Theorem of Calculus, Part 1 If is continuous on [ then the function defined by is differentiable on and The Fundamental Theorem of Calculus, Part 2 If is continuous on then where is any antiderivative of that is, then the function 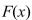a.Use Part 1 of the Fundamental Theorem of Calculus to find b.Use Part 2 of the Fundamental Theorem of Calculus to integrate to obtain an alternative expression for c.Differentiate the expression for found in part (b).The Fundamental Theorem of Calculus, Part 1 If is continuous on [ then the function defined by is differentiable on and The Fundamental Theorem of Calculus, Part 2 If is continuous on then where is any antiderivative of that is, defined by 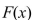a.Use Part 1 of the Fundamental Theorem of Calculus to find b.Use Part 2 of the Fundamental Theorem of Calculus to integrate to obtain an alternative expression for c.Differentiate the expression for found in part (b).The Fundamental Theorem of Calculus, Part 1 If is continuous on [ then the function defined by is differentiable on and The Fundamental Theorem of Calculus, Part 2 If is continuous on then where is any antiderivative of that is, 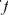a.Use Part 1 of the Fundamental Theorem of Calculus to find b.Use Part 2 of the Fundamental Theorem of Calculus to integrate to obtain an alternative expression for c.Differentiate the expression for found in part (b).The Fundamental Theorem of Calculus, Part 1 If is continuous on [ then the function defined by is differentiable on and The Fundamental Theorem of Calculus, Part 2 If is continuous on then where is any antiderivative of that is, is differentiable on 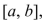a.Use Part 1 of the Fundamental Theorem of Calculus to find b.Use Part 2 of the Fundamental Theorem of Calculus to integrate to obtain an alternative expression for c.Differentiate the expression for found in part (b).The Fundamental Theorem of Calculus, Part 1 If is continuous on [ then the function defined by is differentiable on and The Fundamental Theorem of Calculus, Part 2 If is continuous on then where is any antiderivative of that is, and 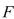a.Use Part 1 of the Fundamental Theorem of Calculus to find b.Use Part 2 of the Fundamental Theorem of Calculus to integrate to obtain an alternative expression for c.Differentiate the expression for found in part (b).The Fundamental Theorem of Calculus, Part 1 If is continuous on [ then the function defined by is differentiable on and The Fundamental Theorem of Calculus, Part 2 If is continuous on then where is any antiderivative of that is, The Fundamental Theorem of Calculus, Part 2 If 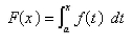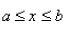a.Use Part 1 of the Fundamental Theorem of Calculus to find b.Use Part 2 of the Fundamental Theorem of Calculus to integrate to obtain an alternative expression for c.Differentiate the expression for found in part (b).The Fundamental Theorem of Calculus, Part 1 If is continuous on [ then the function defined by is differentiable on and The Fundamental Theorem of Calculus, Part 2 If is continuous on then where is any antiderivative of that is, is continuous on 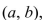a.Use Part 1 of the Fundamental Theorem of Calculus to find b.Use Part 2 of the Fundamental Theorem of Calculus to integrate to obtain an alternative expression for c.Differentiate the expression for found in part (b).The Fundamental Theorem of Calculus, Part 1 If is continuous on [ then the function defined by is differentiable on and The Fundamental Theorem of Calculus, Part 2 If is continuous on then where is any antiderivative of that is, then 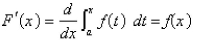a.Use Part 1 of the Fundamental Theorem of Calculus to find b.Use Part 2 of the Fundamental Theorem of Calculus to integrate to obtain an alternative expression for c.Differentiate the expression for found in part (b).The Fundamental Theorem of Calculus, Part 1 If is continuous on [ then the function defined by is differentiable on and The Fundamental Theorem of Calculus, Part 2 If is continuous on then where is any antiderivative of that is, where 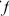a.Use Part 1 of the Fundamental Theorem of Calculus to find b.Use Part 2 of the Fundamental Theorem of Calculus to integrate to obtain an alternative expression for c.Differentiate the expression for found in part (b).The Fundamental Theorem of Calculus, Part 1 If is continuous on [ then the function defined by is differentiable on and The Fundamental Theorem of Calculus, Part 2 If is continuous on then where is any antiderivative of that is, is any antiderivative of that is, 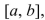a.Use Part 1 of the Fundamental Theorem of Calculus to find b.Use Part 2 of the Fundamental Theorem of Calculus to integrate to obtain an alternative expression for c.Differentiate the expression for found in part (b).The Fundamental Theorem of Calculus, Part 1 If is continuous on [ then the function defined by is differentiable on and The Fundamental Theorem of Calculus, Part 2 If is continuous on then where is any antiderivative of that is, a.Use Part 1 of the Fundamental Theorem of Calculus to find b.Use Part 2 of the Fundamental Theorem of Calculus to integrate to obtain an alternative expression for c.Differentiate the expression for found in part (b).The Fundamental Theorem of Calculus, Part 1 If is continuous on [ then the function defined by is differentiable on and The Fundamental Theorem of Calculus, Part 2 If is continuous on then where 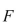is any antiderivative of that is,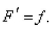

Definitions:

Transformational Leadership

A leadership approach that causes change in individuals and social systems, characterized by inspiring and motivating followers to exceed their own interests for the good of the group or organization.

Transformational Leaders

Individuals who inspire and motivate followers to exceed their own self-interests for the good of the organization and foster significant changes.

Situational Leadership

A leadership theory that proposes the best course of action depends on various situational factors.

Trait Theory

A theory of personality that focuses on the identification and measurement of specific characteristics or traits that influence individual behavior and attitudes.

Related Questions

Q53: The position function of a particle is

Q78: Find an equation of the line tangent

Q103: If <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8680/.jpg" alt="If is

Q120: Evaluate the integral by making the given

Q124: Set up, but do not evaluate, an

Q133: Find two numbers whose difference is 170

Q135: Select the correct graph for the given

Q149: Evaluate the integral. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8680/.jpg" alt="Evaluate the

Q149: The marginal cost function <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8680/.jpg" alt="The

Q158: Given <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8680/.jpg" alt="Given (a)