SCENARIO 15-4 the Superintendent of a School District Wanted to Predict

question 47

Multiple Choice

SCENARIO 15-4 The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test.She obtained the data on percentage of students passing the proficiency test (% Passing) , daily mean of the percentage of students attending class (% Attendance) , mean teacher salary in dollars (Salaries) , and instructional spending per pupil in dollars (Spending) of 47 schools in the state. Let Y = % Passing as the dependent variable, 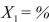Attendance, 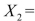Salaries and 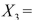Spending. The coefficient of multiple determination ( 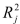) of each of the 3 predictors with all the other remaining predictors are, respectively, 0.0338, 0.4669, and 0.4743. The output from the best-subset regressions is given below: 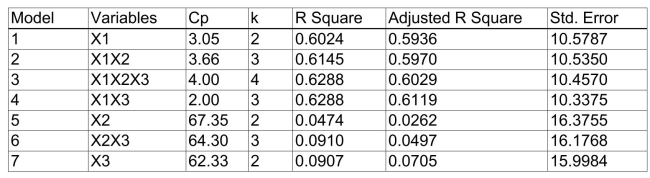Following is the residual plot for % Attendance: 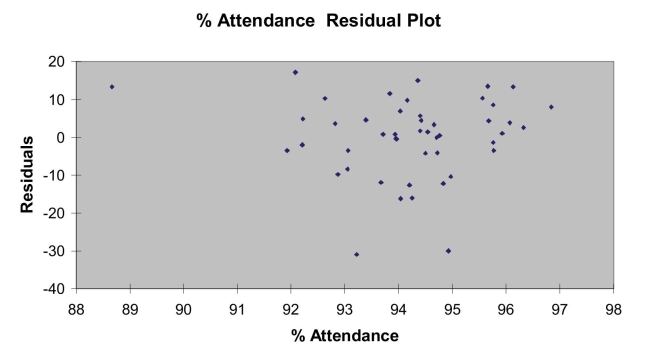Following is the output of several multiple regression models: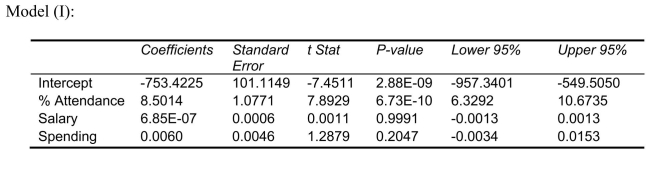
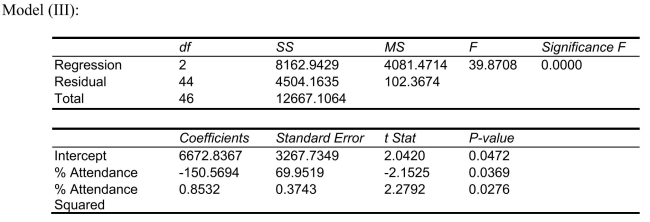
-Referring to Scenario 15-4, the "best" model using a 5% level of significance among those chosen by the 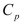statistic is

---

Definitions:

External Frustration

Emotional or psychological stress resulting from blockages or hindrances caused by environmental factors outside an individual's control.

Avoidance-Avoidance Conflict

A psychological dilemma wherein an individual must choose between two undesirable outcomes.

Unfinished Paper

A written document that is not completed, often lacking essential content, conclusions, or final editing.

Failing Grade

An academic assessment outcome indicating that the level of performance did not meet the minimum criteria for passing.