SCENARIO 15-4 the Superintendent of a School District Wanted to Predict

question 17

Multiple Choice

SCENARIO 15-4 The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test.She obtained the data on percentage of students passing the proficiency test (% Passing) , daily mean of the percentage of students attending class (% Attendance) , mean teacher salary in dollars (Salaries) , and instructional spending per pupil in dollars (Spending) of 47 schools in the state. Let Y = % Passing as the dependent variable, 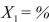Attendance, 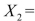Salaries and 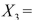Spending. The coefficient of multiple determination ( 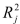) of each of the 3 predictors with all the other remaining predictors are, respectively, 0.0338, 0.4669, and 0.4743. The output from the best-subset regressions is given below: 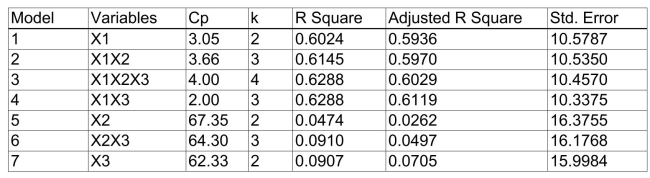Following is the residual plot for % Attendance: 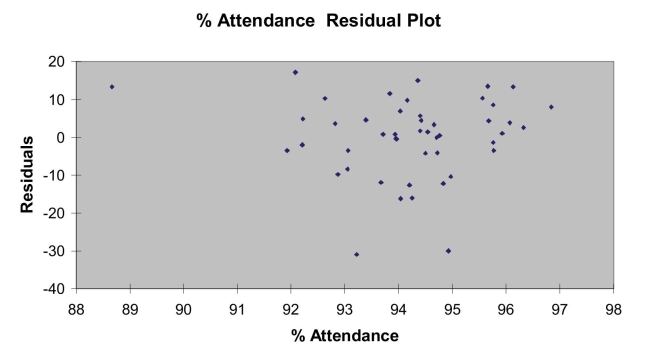Following is the output of several multiple regression models: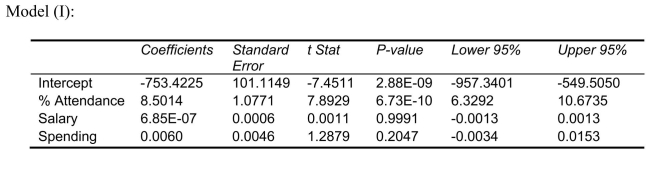
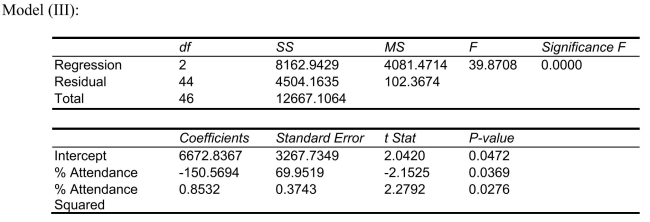
-Referring to Scenario 15-4, which of the following predictors should first be dropped to remove collinearity?

---

Definitions:

Increase Production

The process of raising the output or quantity of goods and services produced by a firm or country.

Nonrefundable Ticket

A ticket purchase that cannot be returned for a refund, often cheaper than refundable options and common in air travel.

Remainder

The amount left over or remaining after division or allocation.

Alternative

An option or choice that is available as a substitute or replacement for something else.