SCENARIO 15-4 The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test.She obtained the data on percentage of students passing the proficiency test (% Passing) , daily mean of the percentage of students attending class (% Attendance) , mean teacher salary in dollars (Salaries) , and instructional spending per pupil in dollars (Spending) of 47 schools in the state. Let Y = % Passing as the dependent variable, 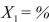 Attendance,
Attendance, 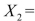 Salaries and
Salaries and 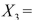 Spending. The coefficient of multiple determination (
Spending. The coefficient of multiple determination ( 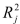 ) of each of the 3 predictors with all the other remaining predictors are, respectively, 0.0338, 0.4669, and 0.4743. The output from the best-subset regressions is given below:
) of each of the 3 predictors with all the other remaining predictors are, respectively, 0.0338, 0.4669, and 0.4743. The output from the best-subset regressions is given below: 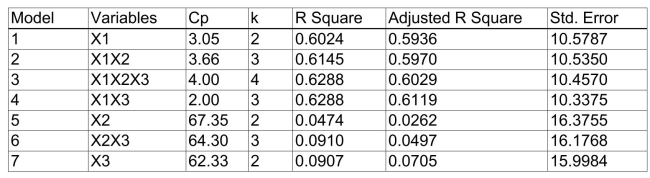 Following is the residual plot for % Attendance:
Following is the residual plot for % Attendance: 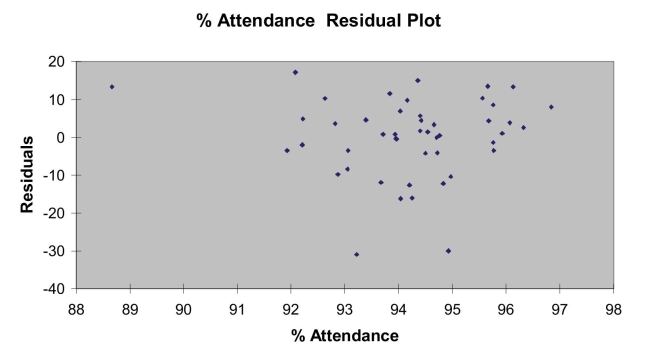 Following is the output of several multiple regression models:
Following is the output of several multiple regression models: 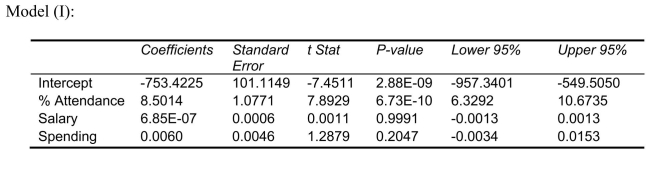

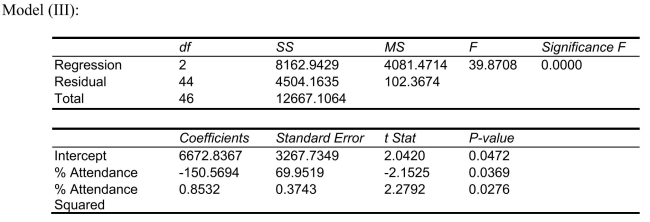
-Referring to Scenario 15-4, the "best" model chosen using the adjusted R-square statistic is
Definitions:
Southern Women
Refers to women living in the southern part of the United States, often discussed in historical and cultural contexts, including their roles, rights, and social expectations.
Southern Patriarchal Society
A societal structure prevalent in the American South characterized by male dominance, traditional family values, and hierarchical social orders.
Institution of Slavery
A legally or socially sanctioned system of forced labor in which individuals are owned, managed, and traded by others.
Social Standing
The position or rank of a person or group within society, influenced by factors like wealth, occupation, and education.
Q2: Referring to Scenario 15-5, what is the
Q3: Referring to Scenario 14-4, which of the
Q24: Referring to Scenario 17-7, the "complete" method
Q73: From an inventory of 48 new cars
Q74: Referring to Scenario 18-8, the null hypothesis
Q82: Referring to Scenario 17-2, the North America
Q88: Referring to Scenario 17-5, the misclassification rate
Q134: Referring to Scenario 13-9, the value of
Q162: Referring to Scenario 16-13, you can reject
Q307: An entrepreneur is considering the purchase of