SCENARIO 18-6 a Weight-Loss Clinic Wants to Use Regression Analysis

question 213

Multiple Choice

SCENARIO 18-6 A weight-loss clinic wants to use regression analysis to build a model for weight-loss of a client (measured in pounds) .Two variables thought to affect weight-loss are client's length of time on the weight loss program and time of session.These variables are described below: Y = Weight-loss (in pounds) 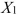= Length of time in weight-loss program (in months) 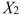= 1 if morning session, 0 if not 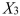= 1 if afternoon session, 0 if not (Base level = evening session) Data for 12 clients on a weight-loss program at the clinic were collected and used to fit the interaction model: 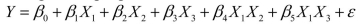Partial output from Microsoft Excel follows: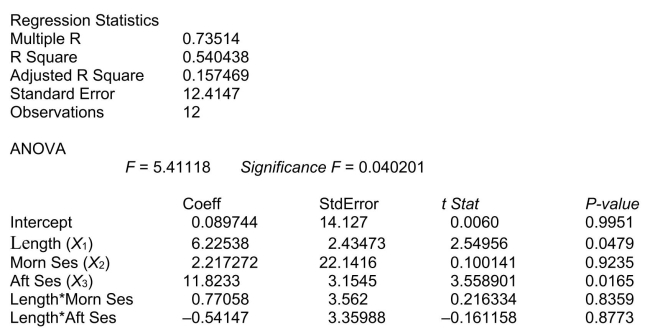
-Referring to Scenario 18-6, what null hypothesis would you test to determine whether the slope of the linear relationship between weight-loss (Y) and time in the program (x₁) varies according to time of session?

---

Definitions:

Annual Coupon

The yearly interest amount paid to bondholders, typically expressed as a percentage of the bond's face value.

Default Risk Premium

The additional yield a lender demands to compensate for the risk that the borrower may default on the loan.

Liquidity Premium

Additional yield that investors demand for holding a security that is not easily traded or sold without a significant price reduction.

Maturity Risk Premium

The extra yield that investors demand to compensate for the risk of holding a bond until its maturity date.