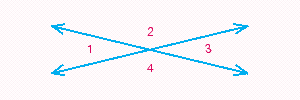
When two lines intersect as in the illustration below, four angles are formed. Angles that are side-by-side, such as 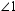 and
and 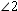 , are called adjacent angles. Angles that are nonadjacent, such as
, are called adjacent angles. Angles that are nonadjacent, such as 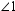 and
and 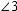 or
or 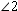 and
and 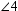 , are called vertical angles. From geometry, we know that if two lines intersect, vertical angles have the same measure. If
, are called vertical angles. From geometry, we know that if two lines intersect, vertical angles have the same measure. If 
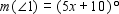 and
and 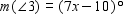 , find x . Read
, find x . Read 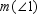 as "the measure of
as "the measure of  ".
". 
Definitions:
Law of Diminishing Marginal Utility
An economic principle stating that as consumption of a good or service increases, the marginal utility derived from each additional unit decreases.
Marginal Utility
Marginal Utility is the added satisfaction or benefit a consumer receives from consuming one more unit of a good or service.
Diminishing Marginal Utility
The principle that the utility or satisfaction gained by consuming each additional unit of a good or service decreases as more of that good or service is consumed.
Marginal Utility
The extra pleasure or benefit derived from consuming an additional unit of a product or service.
Q2: The amount $.15 is written correctly.
Q7: Solve the system by graphing: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBX8672/.jpg"
Q9: Klondik Industries plans to open a new
Q16: The proofreader must make sure that the
Q17: Pick up _ gallons of milk, _
Q17: Ngo Dinh Diem, the U.S.-supported leader of
Q23: The product of two consecutive integers is
Q49: Find the unit price. They charged <img
Q50: Is the number <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBX8672/.jpg" alt="Is the
Q96: What is the classification of the polynomial