Unicellular Yeasts Can Be Represented as Spheres, Whereas Filamentous Hyphae

question 58

Multiple Choice

Unicellular yeasts can be represented as spheres, whereas filamentous hyphae more closely resemble cylinders. As these two geometric figures increase in size, their surface area-to-volume ratios change. The following tables demonstrate how this ratio changes, first for spheres, and second for cylinders. For the cylinder, girth (i.e., radius, r) will remain constant, whereas length, L, will increase. Note the formulas below the respective tables.
A sphere's change in surface area and volume with increasing radius, r

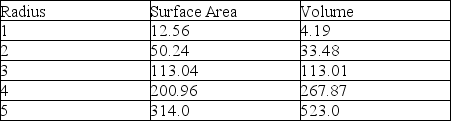
Area of a Sphere = 4r² Volume of a Sphere = 4/3r³
A cylinder's change in surface area and volume with increasing length, L

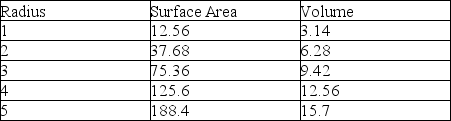
Area of a Cylinder = 2(r²) + 2rL Volume of a Cylinder = r²ᴸ
-As a direct result of increasing surface area in both yeasts and filamentous hyphae, which cell structures/materials must also increase?
1) amount of chitin
2) number of nuclei
3) amount of plasma membrane
4) number of mitochondria
5) amount of peptidoglycan

• A) 1 only
• B) 1 and 3
• C) 2 and 3
• D) 2 and 4
• E) 1, 3, and 5

Evaluating the effectiveness of adoption and enrichment programs on IQ gains.

Comprehending the concept of reaction range and its determinants.

Acknowledging the significance of the environment in shaping intelligence and personality.

Applying the concept of reaction range to various areas of study beyond intelligence.

---

Definitions:

Persuasive

Having the ability to convince or influence someone to believe or do something through reasoning or argument.

That's-Not-All Technique

A sales strategy where an initial offer is improved upon before a decision is made in order to make it more appealing.

Store Manager

A person responsible for overseeing the day-to-day operations of a retail location, including staff management and financial performance.

Prices

The amount of money expected, required, or given in payment for something.